Biomechanics of Fractures and Fracture Fixation

By admin Last updated Apr 18, 2024

Ovid: Rockwood And Green’s Fractures In Adults

Editors: Bucholz, Robert W.; Heckman, James D.; Court-Brown, Charles M.; Tornetta, Paul

Title: Rockwood And Green’s Fractures In Adults, 7th Edition

> Table of Contents > Section One – General Principles: Basics > 1 – Biomechanics of Fractures and Fracture Fixation

Biomechanics of Fractures and Fracture Fixation

Allan F. Tencer

INTRODUCTION

This chapter provides a basic discussion of the concepts
of biomechanics, and demonstrates how these concepts can be used to
understand the basic functions of bone fracture fixation devices and to
avoid clinical problems associated with the mechanics of fracture
fixation. Emphasis has been placed on addressing practical problems.
First, fundamental concepts of mechanics as they apply to the practice
of orthopaedic fracture fixation are explained. This is followed by a
short discussion on the mechanical organization of bone, its ability to
carry load, and the relationship of applied forces and specific
fracture patterns. A discussion of mechanisms of bone and joint injury,
including specific mechanisms observed in car crashes is next
presented. Description of the mechanics of healing bone follows, which
is relevant to understanding the timing of applying progressive load to
healing fractures in patients. Finally, the performance of various
types of fixation systems is discussed, with emphasis on fixation of
difficult fractures, such as the femoral neck and the tibial plateau,
and those involving osteoporotic bone. The focus of the discussion is
not on comparing the various specific devices available, but rather on
demonstrating the common mechanical principles involved in fracture
fixation so that potential problems common to various devices can be
recognized and avoided.

In the study of biomechanics as it relates to fracture
fixation, the fundamental mechanical question remains: is the fixation
system stiff and strong enough to allow the patient early mobility,
before bony union is complete, without delaying healing, creating bone
deformity, or damaging the implant, and yet flexible enough to allow
transmission of force to the healing fracture to stimulate union? The
issue of which brand of fixation is strongest or stiffest is not
specifically addressed because that is not the standard by which
different devices should be judged. Within a range of fixation
stiffness it has been shown that bone will heal, with the amount of
stabilizing callus compensating for more flexible fixation.

BASIC CONCEPTS

Before describing the performance of fracture fixation systems, some basic concepts used in biomechanics will be introduced. As Figure 1-1
demonstrates, loads in many different directions may act on a fixed
fracture, including body weight, and forces induced by muscle
contraction and ligament tension. A force causes an object to either accelerate or decelerate. It has magnitude (strength) and acts in a specific direction, therefore it is termed a vector.
However complex the system of forces acting on a bone, each force may
be separated into its vector components (which form a 90-degree
triangle with the force). Any of several components, acting in the same
direction, can be summed to yield the net or resultant force.
As a simple example, consider the resultant force acting at the
shoe/floor interface during ambulation. It can be separated into a
vertical force because of

P.4

body
weight and a horizontal frictional force that produces the forward
thrust. Similarly, muscle forces can be separated in the same
manner—one force along the axis of the long bone and one perpendicular.
The components of the different forces that act in the same direction
can be added, and the resultant force acting on the bone can then be
found. This concept is important when designing fracture fixation
systems because it allows the designer to size the implants so that
they can withstand the mechanical loads applied without failure.

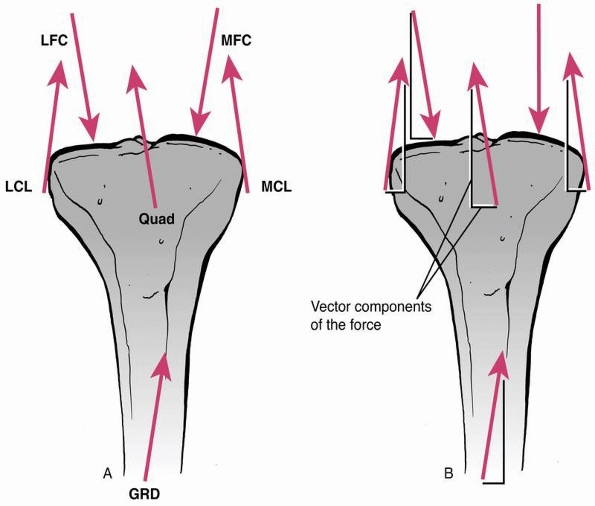
FIGURE 1-1
Force vectors acting on a long bone during functional use as a result
of muscle, tendon, and external forces. A vector indicates that the
force has both magnitude and direction. The complex system of forces
can be divided into components acting perpendicular and parallel to the
ground, or the axis of the bone, then added to arrive at an overall
resultant force.

The two major loads acting on a long bone are those that
cause it to displace in a linear direction (translation) and those that
cause it to rotate around a joint center. Muscles typically cause a
bone to rotate (e.g., the biceps causes the forearm to rotate, the
anterior tibialis causes the foot to dorsiflex). When a force causes
rotation, it is termed a moment and has a moment arm.
The moment arm is the lever arm against which the force acts to cause
rotation. It is the perpendicular distance of the muscle force from the
center of rotation of the joint. As shown in Figure 1-2,
the moment or rotary force is affected not only by the magnitude of the
force applied, but also by its distance from the center of rotation. In
the example, two moments act on the outstretched arm. The weight
carried in the hand rotates the arm downward, while the balancing
muscle force rotates the arm upward. Equilibrium is reached by
balancing the moments so that the arm does not rotate and the weight
can be carried. Note that to achieve this, the muscle force must be 8
times as large as the weight of the object, arm, and hand because its
moment arm or distance from the center of the joint is only one eighth
as long.

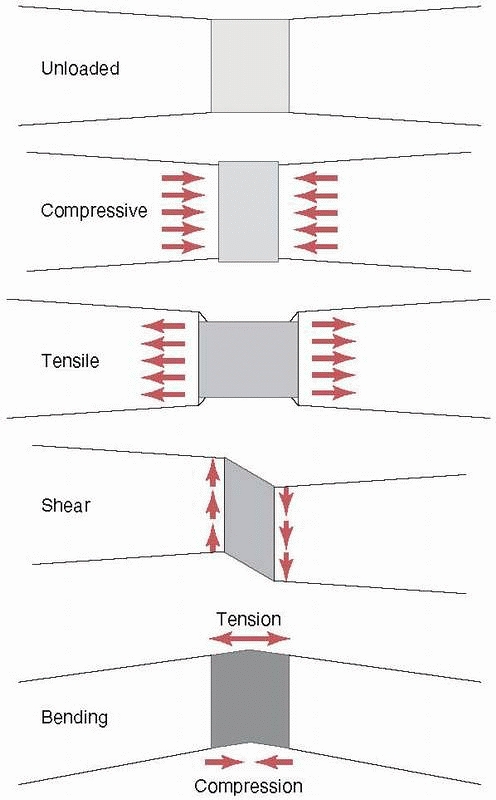
The basic forces—compression, transverse loading, torsion, and bending—cause bone to behave in predictable ways. A compressive force (Fig. 1-3) results in shortening the length of the bone, while tension elongates it. Torsion causes twisting of a bone about its long axis, while bending
causes it to bow at the center. The forces and moments that act on a
long bone during functional use produce three basic stresses on the
healing fracture region: tension, compression, and shear (as shown previously, all forces can be reduced to their basic components). Stress, as shown in Figure 1-4,
is simply the force divided by the area on an object over which it
acts. This is a convenient way to express how the force affects a
material locally. For example, comparing two bones, one with half the
cross-sectional area of the other, if the smaller bone is subjected to
half the force of the larger bone, the stress experienced by each bone
would be the same. Therefore, a smaller woman with less weight

P.5

has
proportionally smaller bones to keep the stresses on the bone tissue
similar to that of a larger and heavier man. The stresses acting on
fracture callus as a result of the different forces are shown (in an
idealized case) in Figure 1-5. Just as stress is normalized force (force per unit area), so can length changes be normalized. Strain
is simply the change in height or length that a bone undergoes during
loading divided by its original height or length, as shown in Figure 1-4.
Under the same force and for bones of similar composition, a bone twice
as long will experience twice the length change. Nevertheless, the
strain will be the same in both cases because the strain (in the longer
bone) will be twice the change in length divided by twice the original
length.

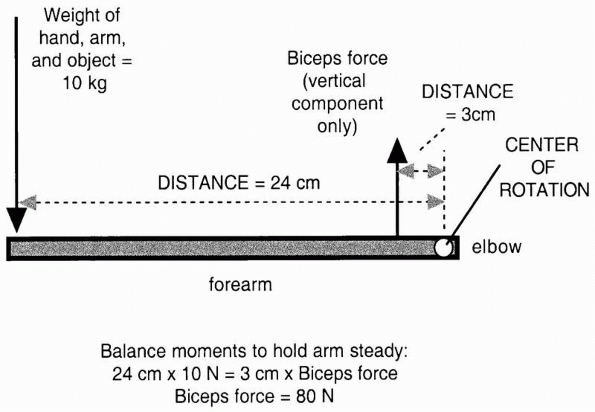
FIGURE 1-2
In this example the outstretched arm is a lever. The moment or load
that rotates the arm downward around the elbow, the center of rotation,
is defined as the product of the weight of the object arm and hand X
distance from the elbow (for simplicity the center of gravity of the
hand, arm, and object are combined). This moment must be counteracted
by a moment in the opposite direction, because of the vertical
component of the biceps muscle acting through its lever, which is
smaller than the lever arm of the weight arm and hand. The biceps force
is then calculated from (10 kg × 24 cm)/3 cm = 80 kg. The biceps force
is much greater than the weight of the object arm and hand because its
lever arm is smaller.

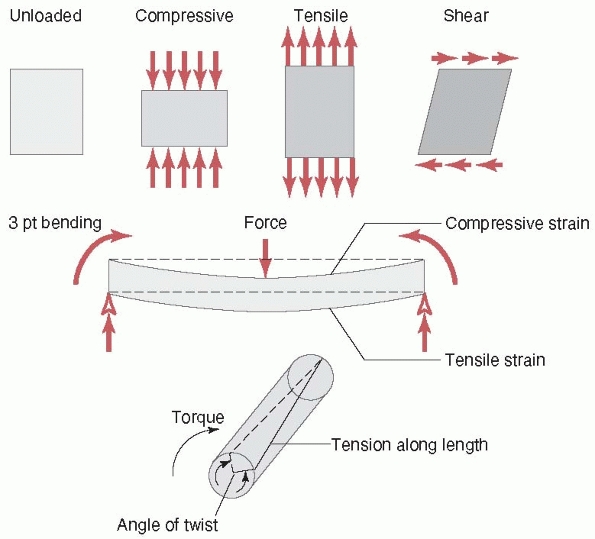
FIGURE 1-3 Top:
Basic forces acting on a long bone and the deflection of the bone in
response. Compression shortens the length, tension increases the
length, and shear deforms the shape of the bone (middle), bending causes the bone to bow, and (bottom) torsion results in twisting about the long axis.

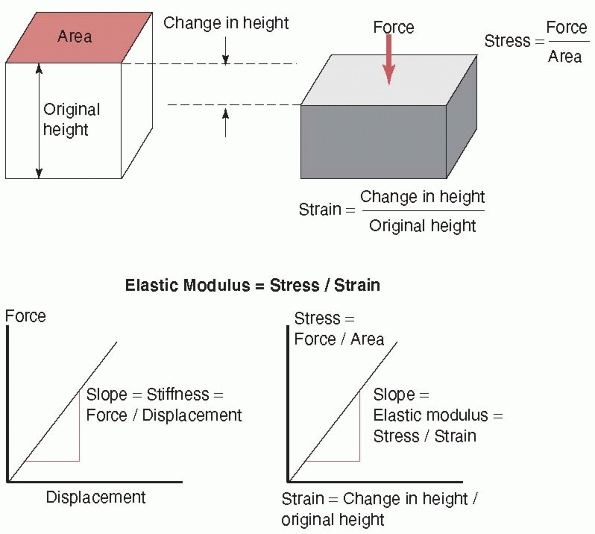
FIGURE 1-4
The stress is defined as the force acting on a surface divided by the
area over which it acts. Strain is the change in height or length of
the object under load divided by its original height or length.
Stiffness is defined as the slope of a force versus displacement graph;
that is, the change in force divided by the corresponding change in
displacement. Elastic modulus is the corresponding slope but of a
stress versus strain graph.

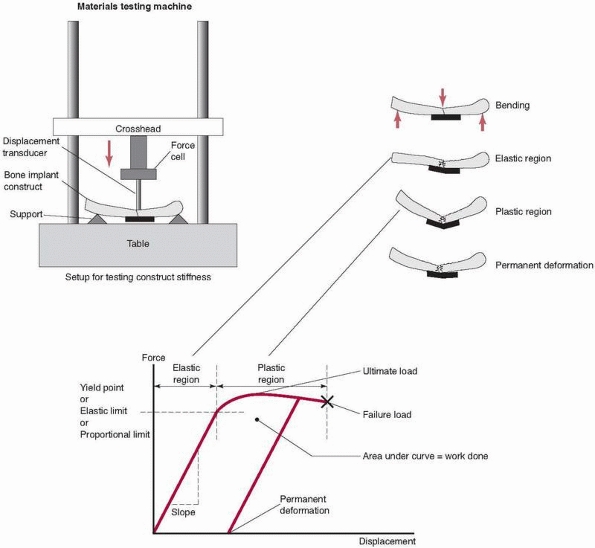
Mechanical testing of fractured long bones with fixation devices applied demonstrates a specific type of behavior, as shown in Figure 1-6. This diagram represents the data measured in an experimental test of the structural properties of the bone-fixation construct; that is, the properties of the fixation device and bone combined. Material properties
relate to the properties of the substances that make up each component
(bone, stainless steel, titanium). As load is applied to the construct
in a testing machine, the construct deforms. This deformation is termed
elastic because when the load is removed,
the construct will return to its original shape (an important
consideration in preventing malalignment of the bone fracture
components). At some load, however, the construct becomes overloaded,
entering the plastic

P.6

range. If the load is released after loading in the plastic range but before failure, some permanent deformation
remains in the construct. Practically, this represents a bent plate,
fixator, or rod and a malaligned fracture. The point at which elastic
behavior changes to plastic is termed the yield point.
The elastic range represents the working range for the fixation
construct. Its two most important properties are its yield point, which
defines its safe maximum functional load, and its stiffness, or the
amount it deforms under load in the elastic range. (A third very
important property, fatigue, will be discussed later.)

FIGURE 1-5
Resulting stresses acting in fracture callus in a idealized case with
each of the basic forces applied (top to bottom): unloaded, compressive
stresses along the bone axis and expansive stresses perpendicular to
the bone axis as a result of compression, tensile and contraction
stresses caused by tension, distortion as a result of shearing; and
tension on the convex side, compression on the concave side, and
internal shearing caused by bending.

Note that a fixation construct may have different yield
points and stiffnesses for loads acting in different directions. An
example is a half-pin external fixator construct applied to a tibia,
with the pins oriented anterior-posteriorly. The stiffness is much
greater in anterior-posterior bending than medial-lateral bending for
this construct. Another property to consider is the work done
in deforming a fixation construct. The product of the force applied and
the distance the construct bends is defined as the work done, and is
represented by the area under the forcedisplacement graph of Figure 1-6. Toughness
can be defined as the work done to fracture a construct or material,
including both the elastic and plastic regions of deformation. A
material may be flexible and tough (e.g., rubber, or a child’s bone
that deforms but is difficult to break) or stiff but brittle (e.g.,
glass, elderly bone), if it cannot absorb much deformation without
fracturing.

The factors that govern stiffness and yield point are
the material from which the fixation device is made and its shape
(considering an ununited fracture in which the fracture callus
contributes little to structural properties). A construct made of
higher elastic modulus materials will be stiffer (for example,
stainless steel as compared to titanium). The stiffness of a construct
is found by dividing the force applied by the deformation that the
construct exhibited. The elastic (or Young)
modulus is determined by dividing the stress applied by the resulting
strain. Unlike whole constructs, in which case it is difficult to
determine stress (because it is hard to define the area over which the
force is applied and at least two different materials are involved),
uniform blocks of materials can be characterized by their elastic
modulus. The moduli of some common orthopaedic materials are given in Table 1-1.
As shown, the elastic modulus of titanium alloy is about one half that
of stainless steel, so given two plates of the same size and shape, the
titanium plate has about one half the stiffness of the stainless steel
plate. This can be important to consider when using new devices made of
different materials.

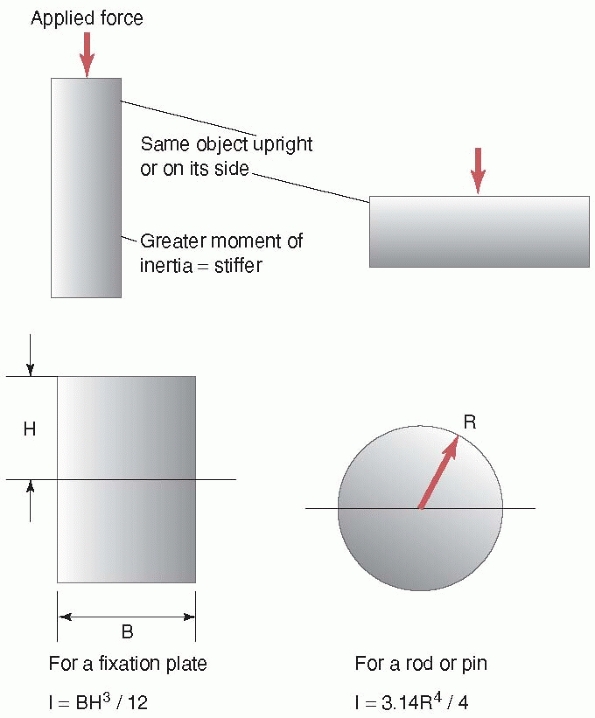
The shape of the implant is important in determining the loads that it can support. As shown in Figure 1-7,
the same wooden 2 × 4 beam that bends easily when load is applied to
its wider surface becomes much stiffer when load is applied to its
narrower surface. This is because, in the latter case, the material of
the 2 × 4 resisting the load is distributed further away from the
center of the beam (note that in this example, the material of the beam
did not change, just its orientation relative to the load applied).
This concept of distribution of material is reflected in the shape
property, moment of inertia. The moment of
inertia provides a measure of how the material is distributed in the
cross section of the object relative to the load applied to it. The
farther away the material is from the center of the beam, the greater
its stiffness. Steel I-beams were developed to take advantage of this
concept; that is, gaining greater stiffness for the same amount of
material. For cylindrical objects like rods, pins, or screws, their
stiffness is related to the 4th power of their diameter. This is why,
as shown in Figure 1-7, for rods made of the
same materials and of similar thickness, a 16-mm diameter
intramedullary rod is 1.7 times as stiff as a 14-mm rod [(16/14)⁴], and a 7-mm diameter pedicle screw is 1.85 times as stiff as a 6-mm diameter screw.

A third important property of a fracture fixation construct is its ability to resist fatigue
under cyclic loading. Load can be applied that remains below the yield
point of the construct, yet progressively creates a crack that grows
until the local stress in the region of the crack exceeds the yield
point and the construct fails. Some materials have an endurance limit
such that they can support a certain level of load indefinitely without
failure. An important aspect to fatigue performance of a fixation
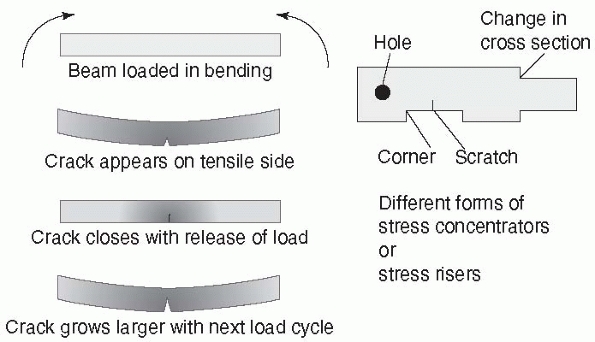
construct is the effect of a stress concentrator.
In completely uniform materials, the stresses, in tension for example,
will be almost identical throughout the material. Fixation devices have
holes, screw threads, and other features in which shape changes occur.
A very radical change in shape (as shown in Figure 1-8,
the sharp corner between threads of different diameter in a fixation
screw) causes a stress concentrator at the corner. This explains why

P.7

the
base of a screw thread, the place at which it meets the shaft of the
screw, has rounded corners. The stresses on a fracture construct are
increased when applied in heavier patients, with poor bone-to-bone
contact across the fracture site, delayed union, early weight bearing
before the fracture has united, and when smaller low-profile fixation
devices are used. For these circumstances, consider the use of larger
implants, taking care not to create stress concentrators by scuffing or
scratching the implant, and delay weight bearing until some fracture
consolidation is apparent. These steps can increase the amount of load
cycles that the implant can bear without fatigue failure.

FIGURE 1-6 Top left:
A fixation construct (bone-fixation-bone) set up in a mechanical
testing machine. In this example a long bone is fixed with a plate and
subjected to bending. Top right: The construct during loading in the elastic region, plastic region, and with permanent deformation. Bottom:
The resulting measurements from the testing machine, which measures
force applied and displacement at the point of the applied load. The
graph demonstrates the elastic region, in which the construct acts like
a spring, returning to its original shape after the load is released;
the plastic region, in which the plate may have permanently bent; and
the failure load, in which the fixation fails.

A scratch can also cause a local small stress concentrator. When immersed in the saline environment of the body, stress corrosion
can occur. Stress corrosion combines the effects of the local growth of
the crack resulting from cyclic loading with galvanic corrosion. A galvanic cell
describes a local environment in which electrons flow from the more
negative to the more positive material when immersed in a liquid
conductor (saline in this case) (Fig. 1-9).
Material is actually removed from the more negative electrode, such as
the surface of the plate during galvanic corrosion. In a fixed
fracture, the dissimilar materials are the surface of the plate (for
example, stainless steel), which

P.8

creates
an oxide surface coating, and the same material within the just opening
crack, which has not yet developed the oxide film. The conductive fluid
is the blood and saline found in the surrounding tissues. Galvanic
corrosion can accelerate the failure of an implant, even when the
implant is loaded well below its yield point, by increasing the rate at
which the crack grows, because along with yielding at the site of the
crack, material at the crack is being removed by the corrosion process.
Another mechanism of corrosion, termed fretting,
results when the surfaces of two implants rub together, such as the
head of a screw against the surface of the plate through which it
passes. Crevice corrosion, which is not
common in modern orthopaedic materials, results from small galvanic
cells formed by impurities in the surface of the implant, causing
crevices as the material corrodes.²³

TABLE 1-1 Basic Engineering Properties of Common Biologic and Implant Materials

Material	Ultimate Strength Tensile (MPa)	Ultimate Strength Compressive (MPa)	Yield Strength 0.2% Offset (MPa)	Elastic Modulus (MPa)
Muscle	0.2
Skin	8			50
Cartilage	4	10		20
Fascia	10
Tendon	70			400
Cortical bone	100	175	80	15,000
Cancellous bone	2	3		1000
Plaster of Paris	70	75	20
Polyethylene	40	20	20	1000
PTFE Teflon	25			500
Acrylic bone cement	40	80		2000
Titanium (pure, cold worked)	500		400	100,000
Titanium (Al-4V) (alloy F 136)	900		800	100,000
Stainless steel (316 L) (annealed)	>500		>200	200,000
Stainless steel (cold worked)	>850		>700	200,000
Cobalt chrome (cast)	>450		>50	20,000
Cobalt chrome (wrought, annealed)	>300		>300	230,000
Cobalt chrome (wrought, cold work)	1500		1000	230,000
Super alloys (CoNiMo)	1800		1600	230,000
(Ultimate tensile strength or maximum force in tension, yield strength at 0.2% offset, the strength at which the strain in the material [change in length / original length] is 0.2%, a usual standard for metals, elastic modulus, or stress/strain.)

FIGURE 1-7 Concept of moment of inertia or the effect of the geometry of an object on its stiffness. Top:
Looking at the edge of a wood 2 × 4 (used in home building); left, the
2 × 4 with the load applied on the narrower side is stiffer than the
same 2 × 4 with the load applied on its wider side. The area of the 2 ×
4 is farther away from the central axis when the load is applied on the
narrower side. Bottom: The moment of
inertia is a term used to describe how the material is distributed
within an object. Left, for a plate, looking at its edge, the moment of
inertia and the stiffness increase directly with the width of the plate
and the cube of its height. For a tube, such as an intramedullary rod,
the moment of inertia increases with the 4th power of its diameter.
Therefore a 16-mm diameter IM rod is 1.7 times as stiff as a 14-mm rod,
and 2.3 times as stiff as a 13-mm rod, if all the rods have the same
thickness and are made of the same material.

P.9

FIGURE 1-8 A stress concentrator is a region of an object in which stresses are higher than in the surrounding material. Left:
Taking the example of a fracture plate subjected to bending, the bottom
surface elongates under load. In the region of highest tensile forces,
a scratch starts to grow into a crack that closes when the load is
released, then reopens slightly larger with the next load cycle,
eventually growing to a point at which the plate fails. Crack growth is
accentuated by stress corrosion, poor bone-to-bone contact at the
fracture, and by loads applied by heavier patients. Right:
Stress concentrators (sometimes referred to as stress risers) occur
around holes, sharp corners, from scratches, and at corners from
changes in cross section.

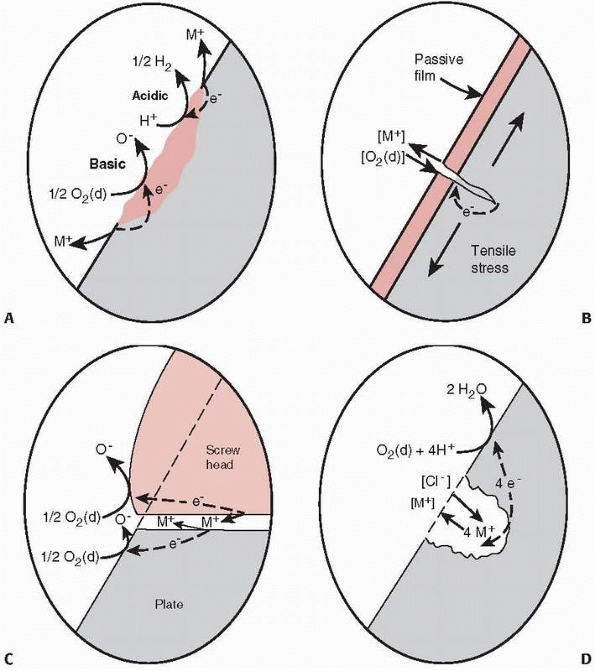
FIGURE 1-9 A.
Illustration of crevice corrosion, with a local galvanic cell caused by
an impurity in the surface of a plate and ions, M+, being released,
resulting in loss of material and formation of a crevice. B.
Stress corrosion occurs by a local galvanic cell setup between the
material at the tip of the crack, which just opened and has not
oxidized, and the remaining oxidized surface of the plate. The released
ions enhance crack growth occurring from loading. C.
Fretting corrosion caused by the loss of the oxide layer on the surface
of a plate caused by rubbing of the base of the screw against the
plate. D. Galvanic corrosion around a scratch or pit in the plate.²³

Another basic property is viscoelasticity.
Biologic materials do not act as pure springs when load is applied to
them. (A spring deforms under load, then returns to its original shape
when the load is released.) For example, if a load is applied to a
tendon, and the load is maintained for a period of time, the tissue
will continue to deform or creep. This is
the basic principle behind stretching exercises. Under a constant load,
a metal fixation plate will deform and remain at that deformation until
the load is removed (elastic behavior). In contrast the tendon both
deforms elastically and creeps, exhibiting both viscous and elastic
behavior. This property has important implications for certain types of
fixation, especially those that rely on loading of

P.10

soft tissues, such as in certain types of spinal fixation (to be discussed later).

A second characteristic of viscoelastic behavior is loading rate dependence.
In simple terms, stretching a soft tissue can be thought of as
stretching two components, an elastic one and a viscous one, which make
up that tissue. For example, consider a spring connected in series to
the handle of a syringe (Fig. 1-10). When a
compressive force is applied, the spring instantly compresses,
representing the elastic response of the tissue. The syringe plunger
starts to displace and continues as it pushes fluid through the
orifice. If the force is held constant, the plunger will continue to
move, representing the viscous creep of the tissue. If the compressive
force is applied slowly, the syringe handle offers little resistance.
As the rate of force application increases, the resistance of the
syringe to motion increases. This represents the increase in stiffness
of the tissue at higher loading rates. That is, the stiffness of the
tissue depends upon the rate at which the load is applied.

A well-known example of loading rate dependence relates
to failure of ligament and bone. At low loading rates, ligament is
weaker than bone and the ligament fails generally in midsubstance. At
higher loading rates, the ligament becomes stiffer, and failure may
occur by avulsion of the bony attachment of the ligament. Stress relaxation
occurs if the applied force, instead of increasing, is held constant.
As the fluid flows out of the syringe, without further movement of the
plunger, the internal force decreases. These three properties—creep,
stress relaxation, and load rate dependence—make up the basic tissue
viscoelastic properties. It should be appreciated that the model used
in this discussion is a simple linear series model, for explanation
purposes only. Nevertheless, more complex models using combinations of
these basic components have successfully described the observed
properties of tissues. Another example of tissue viscoelasticity,
besides tendon and other soft tissues, is found in trabecular bone (for
example, spinal vertebrae). In this case, the trabecular structure acts
as the spring component, while forcing the interstitial fluid through
the porous matrix as the trabeculae deform represents the viscous
component. Under higher loading rates, there is resistance to flow,
increasing the internal pressure and therefore the stiffness of the
structure. These effects have been observed at high loading rates, such
as during fracture (Fig. 1-11).³²

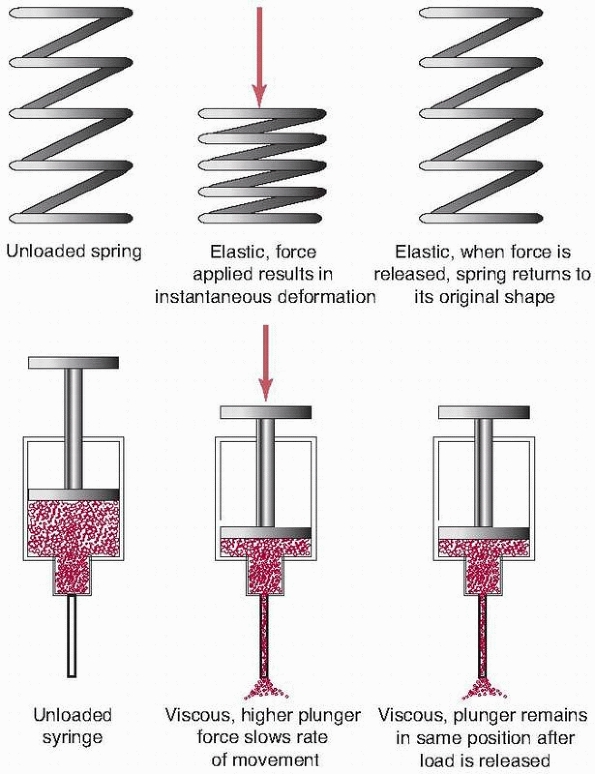
FIGURE 1-10
Viscoelastic response in a biological tissue can be explained by
considering and combining the properties of two devices, a simple
spring and a fluid-filled syringe. The elastic or spring component
instantly compresses when a load is applied to it. When the load is
released, the spring returns to its original shape. When a load is
applied to the viscous component, represented by the syringe, fluid is
forced out the needle. If the load is released, the plunger does not
return, but remains in its final position, representing the creep
property of the tissue. Further, if the force is applied to the plunger
more rapidly, there is greater resistance to motion, explaining the
increased stiffness of tissue to increased rates of loading.
Combinations of these simple components can be used to describe the
mechanical properties of biologic tissues.

In summary, bones and joints can be subjected to various
forces, but these forces can be resolved into basic components that
create tension, compression, shearing, twisting, and bending. These
forces cause internal, compressive, tensile, and shear stresses in the
tissue. The stiffness of a fixation construct used to stabilize a
fracture describes how much it deforms under a given load acting in a
specific direction. Stiffness may vary with direction and is highly
dependent on the shape of the fixation construct. The effect of shape
is described by the moment of inertia. In combination with the moment
of inertia, the elastic modulus of the material describes how stiff the
fixation will be under load, and its ability to withstand the forces
of, for example the patient’s weight during ambulation. Failure of
fixation can come not only from loading above its yield point but also
as a result of repetitive stress. Repetitive loading can cause growth
of a crack at a stress concentrator, and can be significantly
accentuated by corrosion when the implant is immersed in bodily fluids.
Biologic tissues behave viscoelastically; that is, they creep under
constant load, stress relax when the elongation is fixed, and increase
in stiffness as the rate of load application increases.

P.11

In this chapter, these mechanical properties are described in basic units of measurements, defined in Table 1-2.

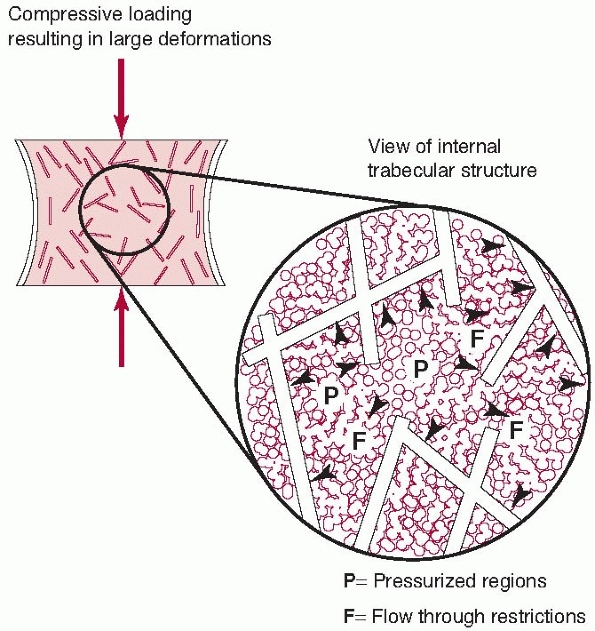
FIGURE 1-11 Trabecular bone possesses some features of the spring and syringe viscoelastic model described in Figure 1-10,
although it should be appreciated that this is an idealized model. The
trabecular structure acts as the spring element. At higher loading
rates, the interstitutial fluid resists flowing through the trabecular
spaces, causing increased internal pressure and greater bone stiffness.
This anatomical feature allows vertebrae and the metaphyseal ends of
long bones to resist dynamic loads caused by rapidly applied forces.³²

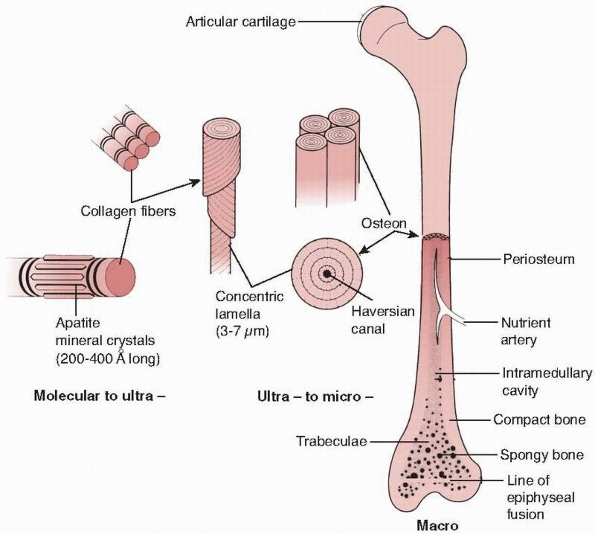
FIGURE 1-12
The hierarchical structure of bone is demonstrated. At the lowest level
of organization, the ratio of mineral crystals to collagen fibrils
determines elastic modulus of the combined material, as shown in Figure 1-13.
At the next level, the fiber orientation is important in determining
the difference in strength of bone in different directions. At the
final level, the lamella of bone fibers form haversian systems that,
particularly in cortical bone, are oriented in the direction of the
major loads the bone must support.

TABLE 1-2 Definitions of the Units Used to Describe the Basic Properties of Fracture Constructs

Force, newtons (N) 1 N ~ 0.254 lb

Displacement, millimeters (mm)

Stress, pressure, modulus, megapascals (MPa) with 1 MPa = force of 1 N/area of 1 mm²

Modulus = stress/strain, in which stress units are MPa; strain has no units

Strain (no units), strain = change in length (mm)/original length (mm)

BIOMECHANICS OF INTACT AND HEALING BONE

Bone has a hierarchical structure. As shown in Figure 1-12,
the lowest level of the structure consists of single collagen fibrils
with embedded apatite crystals. At this level of structure, changing
the collagen to mineral ratio has a significant effect on the elastic
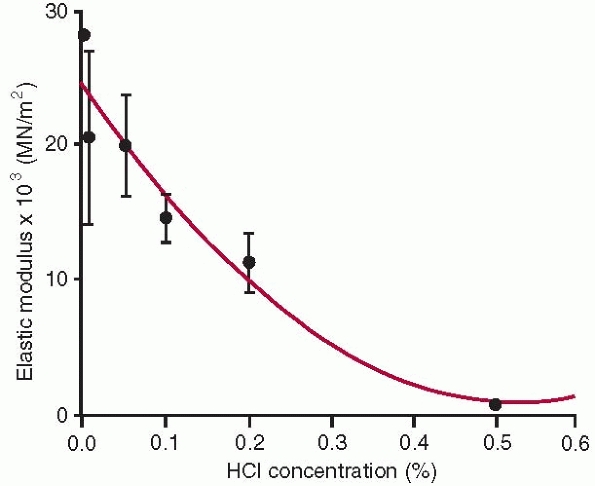
modulus of bone,³⁰,³²,⁴² because it decreases with loss of mineral (Fig. 1-13).
This is important from a fracture healing perspective because
mineralizing healing callus goes through phases of increasing mineral
density and corresponding increased modulus as healing occurs. At the
next level of structural organization, the orientation of the collagen
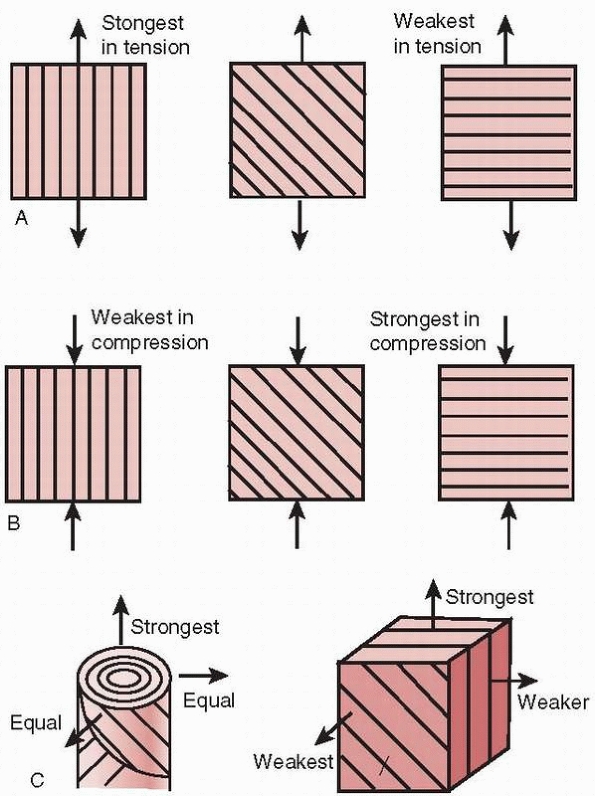
fibrils is important.⁹,¹⁰,¹¹,¹²,⁵⁵,⁵⁶,⁵⁷ As demonstrated in Figure 1-14, the orientation of its fibers affects the ability of bone to support loads in specific

P.12

directions. During fracture healing, the callus initially starts as a
disorganized random array of fibers, which progressively reorganize to
become stiffest along the directions of the major applied loads (body
weight and muscle forces) to which the bone is exposed. At the next
level, the density of the haversian systems affects bone strength. It
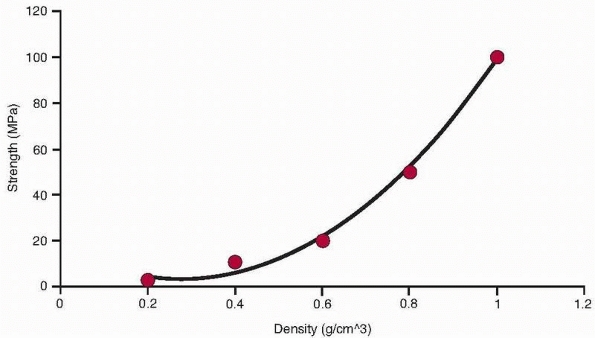
has been repeatedly demonstrated that a power law relationship exists
between bone density and strength at this level of structure (Fig. 1-15).
This means that as bone density decreases, its strength decreases as
the square of its density (as density decreases by half, strength
decreases by a factor of 4). This forms the basis for predicting
changes in bone strength as a result of conditions such as
osteoporosis. Similarly, the modulus changes with bone density by a
power of between 2 and 3.¹⁹,²¹,²⁹,³⁵,⁶²
Noninvasive measures of bone density such as quantitative computed
tomography (qCT) have been shown to have a significant predictive
relationship to bone strength.³,⁴³,⁴⁴,¹⁰³

FIGURE 1-13
Elastic modulus of bone samples tested in tension after exposure to
different concentrations of HCl. Greater HCl concentration
progressively demineralizes bone, ultimately leaving only collagen.
This diagram illustrates the contribution of bone mineral to the
tensile elastic modulus of whole bone.³⁰

FIGURE 1-14 Effects of collagen fiber direction on the resistance to loads applied in different directions. A. Under tensile loading, the strongest arrangement is having the collagen fibers parallel to the load. B. Under compressive loading, the strongest arrangement is having the collagen fibers perpendicular to the load. C.
In bone that must accommodate different loading directions, the
arrangement of the haversian system produces one strongest direction
along the axis, with proximately equal strengths in other directions.⁵⁷

Several additional factors can affect the strength of
bone. As discussed previously, bone is a viscoelastic material whose
strength and modulus both increase as loading rate increases (for
example, in fracture impact loading as compared with normal ambulation).²⁹,³⁸,³⁹,⁴⁰,¹⁰⁸,¹⁶³
The geometry of bone, specifically the size of the cross section and
thickness of the cortex, affects its moment of inertia and therefore
its strength.¹²⁴ Age also affects
bone properties. The bending strength and modulus increase as bone
mineralizes and matures from childhood to adulthood and slowly decrease
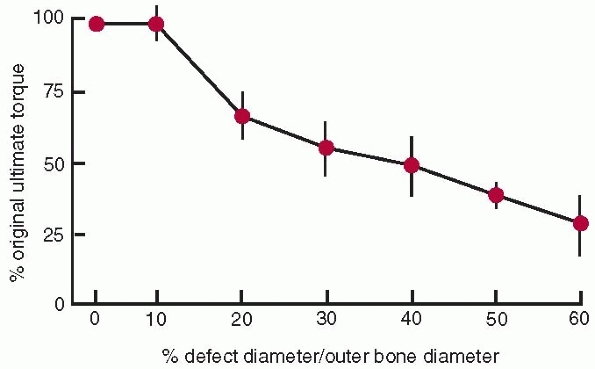
thereafter³⁹,⁴³,¹⁵⁷ and the capacity to absorb impact energy decreases with age⁴¹ as bone becomes more brittle. Defects or holes in bone (for example from drilling for screws) also affect its strength.²⁷,³⁰,⁴⁷,⁹⁷,¹⁰⁶ The torsional strength of bone decreases as the diameter of the hole or defect increases (Fig. 1-16).
As the hole increases in size to 30% of the diameter of the bone, bone
strength decreases to about 50% of that of the bone without a defect.
An important consideration, applicable in the resection of bone (such
as in removal of a tumor) is the shape of the hole or defect left after
tumor removal. Leaving a hole with square corners significantly
decreases bone strength compared to the same hole with rounded corners,
because the square corner is a large stress concentrator. Oval or
circular holes, while themselves still stress risers, do not contribute
the additional effect of the sharp corner.³⁴ Table 1-3 summarizes the strength of cortical and cancellous bone material as well as the ultimate strengths of various whole bones.

As a fracture heals, its strength is affected by changes
in its mineral content, callus diameter, and fiber organization, as
discussed previously. The initial callus forms from the periosteal
surface outward, which is beneficial mechanically, because as the outer
diameter of the healing area enlarges, its moment of inertia and
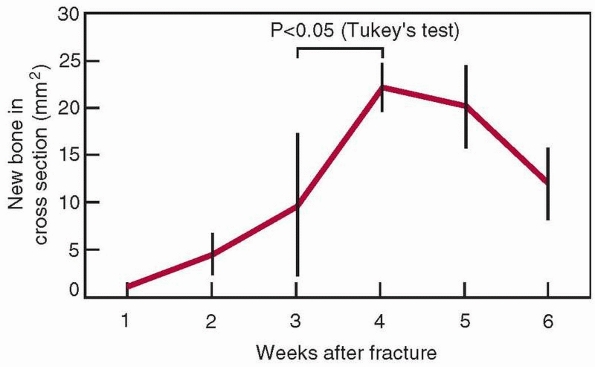
therefore its initial stiffness both increase, as shown in Figure 1-17.¹²² The cross-sectional area increases progressively, as shown in Figure 1-18, as does the mineral content of the callus.⁸ The mechanical results of these changes to bone as the fracture heals are shown in Figure 1-19.
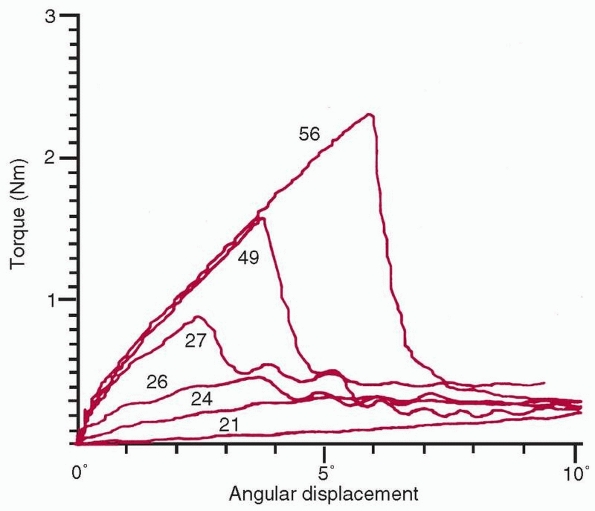
From torsional tests of healing rabbit long bones, progressive
increases were observed in stiffness and peak torque to failure with
time.¹⁵⁹ Interestingly, in that
experiment, the stiffness appeared to gain normal values before the
peak torque to failure, showing that stiffness and strength are related
but not directly. Figure 1-19 shows that beyond 4 weeks (in rats, whose bones heal rapidly),

P.13

the cross-sectional area starts to decrease as the bone remodels to normal shape, while the bone tissue continues to mineralize.

FIGURE 1-15
The relationship of trabecular bone density to compressive strength and
modulus demonstrates a power law relationship so that these properties
decrease by a factor of about 4 when density decreases by half.³²

The mechanical environment created by the fixation
system along with the available blood supply affects the type of tissue
formed in a healing fracture. The theory of interfragmentary strain
attempts to relate the types of tissues formed to the amount of strain
experienced by the tissue between the healing bone fragments.¹²²
This theory is a simple representation and cannot describe the complex
stresses that the tissue is exposed to during actual healing.
Nonetheless, within the limitations of the theory, when large strains
occur in the tissues between healing bone surfaces, granulation tissue
is formed. Intermediate level strains produce cartilage and small
strains result in primary bone healing, or direct deposition of bone
tissue with limited callus formation.

FIGURE 1-16
The relationship of ultimate torque (failure torque) of a long bone to
the diameter of the hole divided by the outer diameter of the bone.
There is no change in ultimate torque until the defect size increase
beyond greater than 10% of the diameter of the bone.⁴⁷

Among the limitations of this theory, one should
recognize that it doesn’t follow that zero strain will result in
maximum bone formation. Load and some resulting strain are necessary
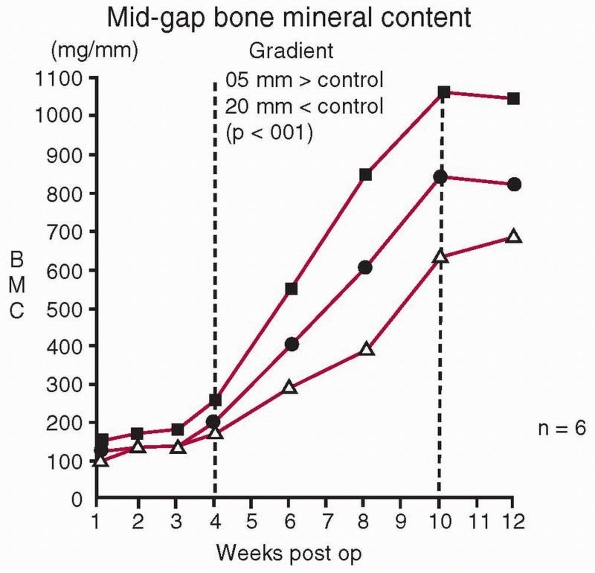
within the healing fracture to stimulate bone formation. In a study in
which controlled daily displacements in compression were applied to
healing long bones using an external fixator, and the bone mineral
within the healing fracture was measured with time, there was an
optimal displacement above or below which less mineral was created in
the fracture callus (Fig. 1-20).¹⁵⁸ Further, compression rather than tension is the preferred direction of loading.¹⁶
Fracture fixation constructs of different stiffnesses within a certain
range produce healed fractures with similar mechanical properties,
however, they may reach this endpoint by different routes. In a study
of femoral fixation using intramedullary rods of either 5% or 50% of
the torsional stiffness of the intact femur, the femurs fixed with the
lower stiffness rods produced an abundance of stabilizing callus, as
opposed to the femurs with more rigid fixation, see Figure 1-21.
This is because with more rigid fixation there was less necessity for
biological fracture stabilization. In both cases, however, the
mechanical properties of the healed fractures were ultimately similar.¹⁶²
These studies demonstrate that some strain as a result of loading the
fracture stimulates healing, and that bone will adapt and heal within a
relatively wide range of mechanical stability environments.

In summary, several factors affect the strength of bone
and healing fractures. Increasing mineral content increases fracture
stiffness. Callus that forms on the periosteal surface is beneficial in
increasing the moment of inertia and therefore the stiffness of the
fractured region. Healing fractures exhibit several stages, with
stiffness returning to normal followed later by peak load to failure.
Bone will heal within a range of mechanical environments. To a certain
extent, healing bone will compensate for more flexible fixation by
forming a greater quantity of fracture callus; however, there is a
range of loading of a healing callus, sufficient to stimulate bone
formation, which increases as the callus matures.

BIOMECHANICS OF BONE FRACTURE

To appreciate why bone fractures in certain patterns, one must understand that, as shown in Table 1-3, bone is weakest in

P.14

tension and strongest in compression. Therefore, when a force creates
tensile stresses in a particular region of a loaded bone, failure will
generally occur first in that region. The simplest example, shown in Figure 1-22,
is the transverse fracture created in a long bone subjected to pure
bending. Because in this example the upper, convex surface undergoes
the greatest elongation, it is subjected to the largest tensile
stresses, and failure, indicated by a crack, initiates here. The crack
then progresses transversely through the material, and layers just
below the outer layer become subjected to high tensile stress until
they crack as well. In this manner, the crack progresses through the
bone transversely until it fails. The concave surface is subjected to
compression so the crack does not initiate there. A second example is
the fracture line or crack that occurs when a bone is subjected to
torsion or axial twisting. In those cases, a spiral fracture results.
Consider, as shown in Figure 1-22, a
rectangular area on the surface of a long bone that is loaded in
torsion. The rectangle distorts as the bone twists, with one diagonal
of the rectangle elongating and the other shortening, depending on the
direction of twist. A crack will form perpendicular to the diagonal
that is elongating, and progresses around the perimeter of the bone
resulting in a spiral fracture. The region of bone with the smallest
diameter is usually the least stiff region, resulting in the greatest
distortion of the surface and is generally the location of the
fracture. This explains why torsional fractures of the tibia often
occur in the narrow distal third, see Figure 1-23.

TABLE 1-3 Mechanical Properties of Bone Material and Whole Bones in Different Loading Directions

Bone Type	Load Type	Elastic Modulus (×10 E9 N/m²)	Ultimate Stress (× 10 E6 N/m²)	Reference
Cortical	Tension	11.4-19.1	107-146	Evans Acta Anat 1958;35:285 Evans Am J Anat 1967;120:79 Kotani Spine 1999;24:1406 Wright Med Biol Eng 1976;14:671 Reilly, J Biomech 1974;7:271
	Compression	15.1-19.7	156-212	Curry 1984, Princeton University Press
	Shear		73-82	Yamada 1970, Williams and Wilkins
Cancellous	Tension	~0.2-5.0	~3-20	Curry J Biomech 1976;12:459
	Compression	0.1-3	1.5-50	Carter J Bone Jt Surg 1977;59A:954 Weaver J Bone Jt Surg 1966;48A:289 Galante Calcif Tissue Res 1970;5:236
	Shear		6.6 +/- 1.7	Stone J Biomech 1983;16:743
Bone Type	Loading Direction and Type		Ultimate Strength	Reference
Cervical spine	Axial compressive impact		980-7400N	Kotani Spine 1999;24:1406 McElhaney Soc Auto Eng 1983;83:1615 Nusholtz 25th STAPP car crash conf 1981:1197 Yoganandan J Spinal Disorders 1991;4:73
	Extension		57 N-m	Nahum Accidental Injury 1993 Springer-Verlag
	Flexion		120 N-m	Nahum Accidental Injury 1993 Springer-Verlag
	Lateral Bending		54 N-m	Nahum Accidental Injury 1993 Springer-Verlag
Lumbar Spine	Axial compressive impact		1400-9000 N	Bell Calcif Tissue Res 1967;1:75 Brassow Eur J Radiol 1982;2:99 Cody Spine 1991;16:146 Hansson Spine 1980;5:46 Halton J Anat 1979;129:753 Tran Spine 1994;20:1984
Sacroiliac Joint	Axial compressive impact		3450-3694 N	Fasola 1955; Wright Patterson AFB
Femoral neck	Lateral to medial at trochanter		1000-4000 N	Smith J Bone Jt Surg 1953;35A:367
	Vertical impact at femoral head		725-10,570 N	Alho Clin Orthop 1988;227:292 Leicher Clin Orthop 1982;163:272 Stankewitz J Orthop Res 1996;14:786
Femur	Torsion		183 N-m	Martens J Biomech 1980;13:667
	From impact at knee along axis		6230-17,130 N	Patrick 9th STAPP car crash conf 1966:237 Viano J Biomech 1980;13:701
	Three-point bending, posterior		21.2-31.3 N-m	Mather J Biomech 1968;1:331
Patella	Impact perpendicular to anterior		6900-10,012N	Patrick 9th STAPP car crash conf 1966:237
Tibia	Axial torsion		101 +/- 35 Nm	Martens J Biomech 1980;13:667
Foot and ankle	Impact perpendicular to sole		4107-6468 N	Assal 46th AAAM 2002:273 Yoganandan Soc Auto Eng 1996;96:2426 Schueler In Soc Auto Eng 1996;PT-56:551 Kitagawa Soc Auto Eng 1998;983145 Funk Soc Auto Eng; 2000;2000-01-0155 McMaster; STAPP car crash conf 2000;44:357

P.15

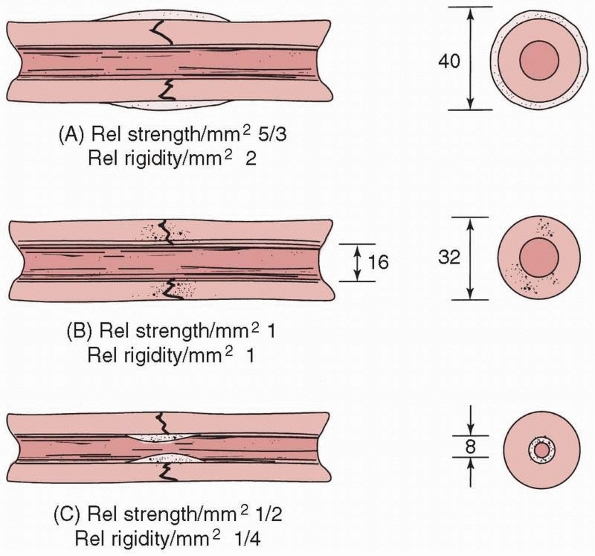
FIGURE 1-17 A comparison of the moments of inertia and resulting strengths when fracture callus is located (A) on the outer surface, (B) on the bone surfaces, or (C)
in the medullary canal. The strength and rigidity are significantly
increased when callus is located over the periosteal surface, compared
to within the medullary canal.¹¹⁸

FIGURE 1-18
Changes in the cross-sectional area of a healing femoral fracture,
which peaks and slowly decreases. There is a similar increase in the
mineral content. (The data come from rats, which heal more rapidly than
humans, indicated by the 4-week time to peak mineralization.⁸)

FIGURE 1-19
A comparison of superimposed torque-angular displacement plots taken
from experimental long bones at different stages of healing shows the
significant increase in both stiffness and peak torque to failure with
increased duration of healing. Numerical values are time in days
postfracture in rabbits.¹⁵⁹

FIGURE 1-20
The effect on bone mineral of different cyclic displacements applied
daily within a healing fracture (upper curve, 0.5 mm; middle curve, 1.0
mm; lower curve, 2.0 mm for 500 cycles/day). This shows that some
displacement (in this experiment, 0.5 mm) stimulates bone formation,
but that greater displacements (1.0 mm and 2.0 mm) do not enhance bone
formation. These results point to an optimal range of displacements for
maximum bone formation.¹⁵⁸

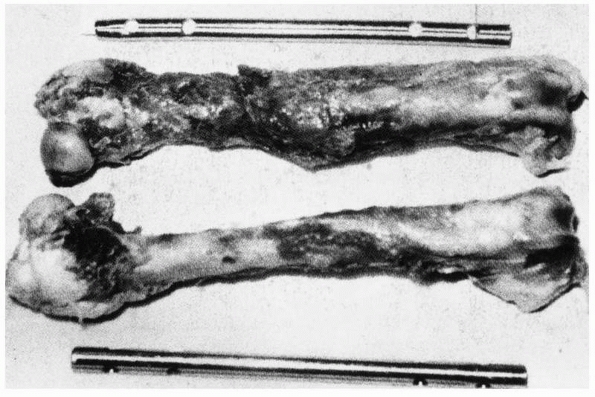
FIGURE 1-21 A comparison of the different healing responses of dog femurs with midshaft fractures fixed with (top) IM rods of 5%, or (bottom)
50% of the torsional stiffness of the intact femur. The femurs fixed
with rods of lower stiffness produced more callus as additional
stabilization against functional loads, but there was ultimately no
difference in mechanical properties between the femurs fixed with rods
of different stiffnesses.¹⁶²

P.16

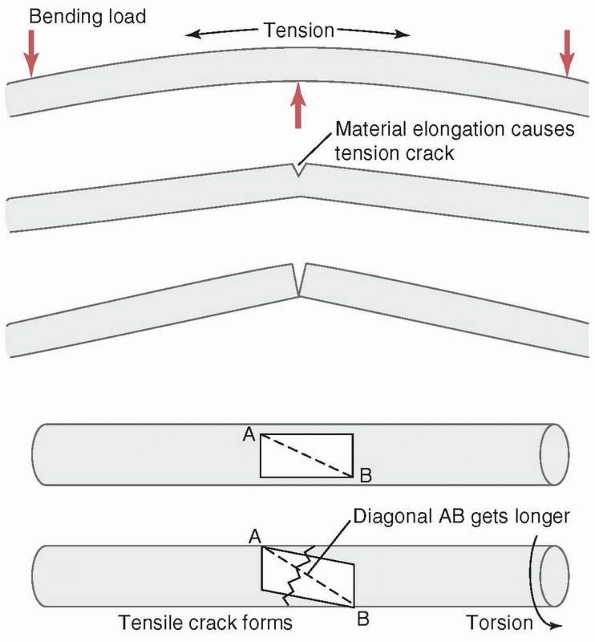
FIGURE 1-22 Top:
A transverse fracture is created by the progressive tensile failure of
bone material starting from the convex surface in which elongation and
therefore stress is greatest, with the crack progressing to the concave
side. Bottom: A spiral fracture is created
by the progressive failure in tension of fibers on the bone surface
along the diagonal that elongates as the material on the surface
distorts when torque is applied. (A rectangle on the surface becomes a
parallelogram, with one diagonal elongating. The crack will be
transverse to the diagonal.)

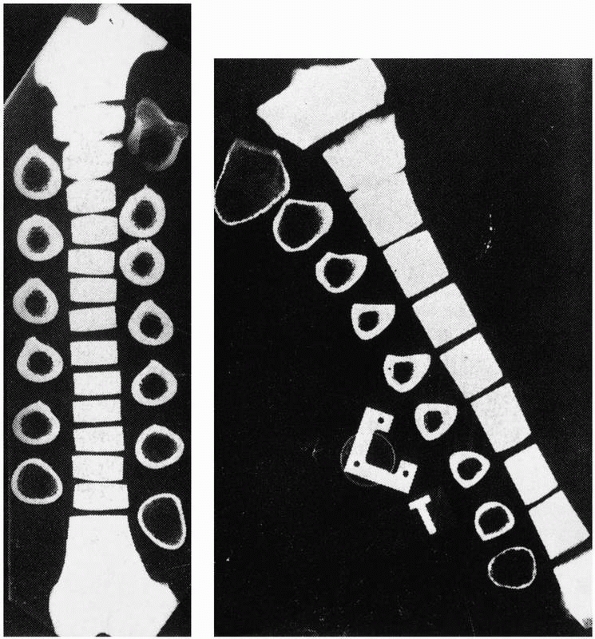
FIGURE 1-23 Cross sections through (left) a femur, and (right)
a tibia. The small cross section of the distal third of the tibia
results in more distortion and higher stresses and explains why
torsional failure often occurs in this area.

A compressive load results in failure of cortical bone
by shear, indicated by slippage along the diagonal, because bone is
weaker in shear than in compression (Fig. 1-24).
In this case, compressive loading causes an interface within the bone
at 45 degrees to the applied load to slide along another at an oblique
angle. At very high loads, such as during impact fractures, crushing or
comminution of bone also occurs, especially at the weaker metaphyseal
ends of a long bone. The trabecular bone at the metaphyseal ends is
weaker in compression than the diaphyseal cortical bone is in shear.
Because of this, it is unlikely that shearing failure will occur in the
diaphysis caused by pure compressive forces. The butterfly fracture (Fig. 1-24)
results from combined bending and compression. Bending load causes the
fracture to start to fail in tension producing a transverse crack, but
as the crack progresses and the remaining intact bone weakens, it
starts to fail in compression, causing an oblique (shear) fracture
line. As the ends of the failing bone are driven together, a third
fragment—the butterfly—may result as the

P.17

oblique
fragment splits off. The production of a butterfly fragment probably
depends on the timing and magnitude of the two basic applied loads:
compression and bending.

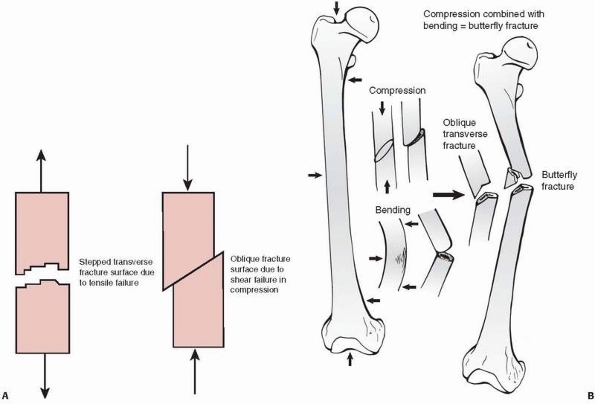
FIGURE 1-24 A. Left:
Tensile fracture causes a stepped surface as fibers pull apart. The
crack progresses, then steps to an adjacent region in which failure
continues. Right: Pure compression of
cortical bone results in failure by shearing or sliding along oblique
surfaces. In reality, pure compression of a long bone (in a fall for
example) results in crushing of the much weaker metaphyseal trabecular
bone with a pilon fracture of the distal tibia or a tibial plateau
fracture as the result. B. Some fractures
that combine bending and compression demonstrate transverse cracking as
a result of bending followed by an oblique crack characteristic of
compressive failure. The butterfly fracture with additional splitting
of the fragment secondary to the initial fracture is an example.

Aging, especially with osteoporotic changes, alters the
force required to fracture bone and the types of fractures that occur.
As shown in Figure 1-15, trabecular bone
stiffness varies with the cube (3rd power) of its density and strength
approximately with the square of its density.³²
Bone mass normally peaks around age 25 to 30 years and decreases up to
1% annually thereafter. If the density of trabecular bone is decreased
by 30% in a 60- to 70-year-old as a result of osteoporosis, the bone
compressive strength is about half of that of a 30-year-old. Typically,
fractures as a result of osteoporosis occur in the vertebrae, the
distal radius, and the femoral neck. In addition, osteoporosis changes
the cross-sectional shape of long bones, decreasing thickness by
increasing the endosteal diameter while causing the periosteal diameter
to increase. If cortical outer diameter—for example, in the
femur—increased and cortical thickness decreased at the same rate, the
moment of inertia of the bone cross section would be larger. That is
why large-diameter thin tubing can be substituted for smaller diameter
thicker tubing in structures (for example, sailboat masts), saving
weight while not sacrificing strength. However, in the femur, the inner
surface of the cortex also becomes more irregular and porous,
decreasing its material strength. A common result of loss of femoral
bone mass combined with other factors, such as poor balance, is a hip
fracture usually resulting from a fall.¹

Auto crashes account for many fractures. Some particular
mechanisms have been observed. Fracture of the calcaneus or the
malleoli of the foot and ankle can occur through a combination of the
foot being forced against the brake pedal by the weight of the occupant
during a high speed frontal collision, or in combination with the floor
pan of the auto crushing into the space in which the foot resides.¹²⁷
Drivers who were braking during a crash were shown to be much more
likely to injure their right foot compared with their left foot.¹⁵
If the Achilles tendon applies load to resist the forced dorsiflexion
of the foot on the brake pedal, the combination of these two loads make
cause three point bending loading of the calcaneus, with the posterior
facet of the talus as the fulcrum. A crack initiates on the plantar or
tensile side of the calcaneus and a tongue type calcaneus fracture can
occur. Inversion or eversion, in which the foot is not securely planted
on the brake pedal and rotates with compression, is likely to result in
a malleolar fracture,⁶¹

P.18

although the combinations of forces causing these high energy fractures are not entirely predictable.

A major mechanism of midshaft femur fractures is impact
with the dashboard of the vehicle in a frontal collision, especially
for unrestrained drivers who submarine or slide forward in the seat.¹⁵⁴ Tensing the quadriceps and hamstrings muscles during a crash applies significant additional compression along the femur.¹⁵⁴
The anterior bow of the femur causes the external compressive force
from contact of the knee with the dashboard, and internal muscle forces
to bend the femur, resulting in bending and transverse or oblique
fractures. If the femur of the occupant hits the dashboard in an
adducted orientation, the femur can be displaced from the acetabulum,
causing a fracture of the acetabular roof and dislocation of the hip
joint. Pelvic fractures result from loading in side impact crashes, in
which the door punches inward against the hip and pelvis. The actual
fracture pattern (symphysis, sacroiliac joint, or both) is probably the
result of the specific alignment of the pelvis with the applied loads
at impact. Pelvic fracture classifications are based on the presumed
mechanism of injury and specific forces applied.¹³⁹,¹⁴¹,¹⁶⁶,¹⁶⁷
Bilateral hip fractures have been found to occur in crashes in which
the vehicle has a large center console that tends to trap the pelvis as
force is also applied on the hip opposite that which contacts the door.
Auto crashes also create, in occupants with lap but not shoulder belts,
the classic “Chance fracture,” which is combined compression and
flexion failure of a lumbar vertebra, usually at the level in which the
lap belt forms a fulcrum. Upper extremity injuries in auto crashes have
been found to be related to airbag deployment and entrapment of the arm
in the steering wheel.⁶⁵

BIOMECHANICS OF FRACTURE IMPLANTS

Avoiding Mechanical Problems with Fracture Fixation Devices

In this section, the functions of commonly used fixation
devices for skeletal fracture fixation are discussed. Observed fixation
problems with devices such as wire, cable, screws plates, IM rods, and
external fixators are explained with the objective of reducing the
potential for mechanical damage or failure of these devices during use.

Cerclage Wire Breakage

The tensile strength of surgical wire has been shown to increase directly with its diameter,¹⁵⁰ and when twisted, the optimal number of turns is between four and eight.¹³²
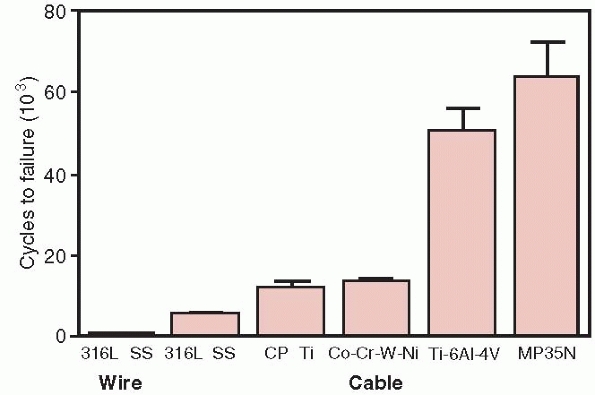
However, solid wire is very sensitive to notches or scratches. Testing
shows that notches as small as 1% of the diameter of the wire can
reduce its fatigue life by 63%.¹³²
For this reason, cable has been introduced for cerclage applications.
Cable has significantly better fatigue performance compared to wire, as
shown in Figure 1-25.⁶⁴
Because cables consist of multiple strands of single thin wires, damage
to any particular strand does not result in failure of the whole cable.
Single loops of suture such as Ethibond are about 30% as strong as
18-gage stainless steel wire in tension, and Merseline tape is about
50% as strong. Four loops of Ethibond were shown to have tensile
strength equivalent to stainless steel wire.⁷⁰

FIGURE 1-25
A comparison of the fatigue resistance of wire and cables made of the
indicated materials. Wire, 316 SS (stainless steel), cable 316 SS, Cp
Ti, commercially pure titanium, Co-Cr-W-Ni, cobalt chrome, Ti 6Al 4V,
titanium alloy, MP35N, nickel alloy.⁶⁴

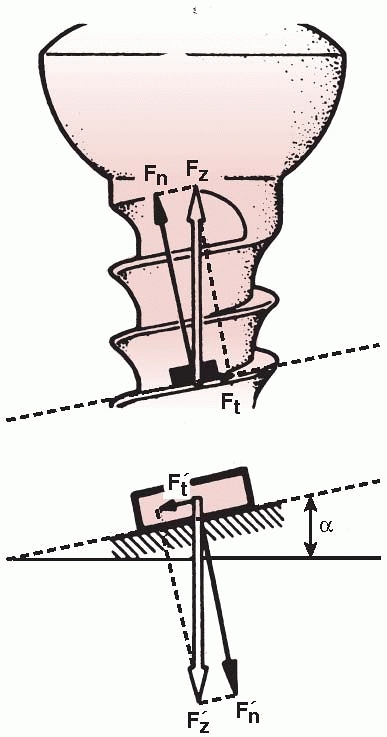
Screw Breakage by Shearing during Insertion

A screw is a mechanical device that is used to convert
rotary load (torque) into compression between a plate and bone, or
between bone fragments. As shown in Figure 1-26,
the thread of a screw, if unwound from the shaft, is really a ramp or
inclined plane that pulls, for example, underlying bone toward

P.19

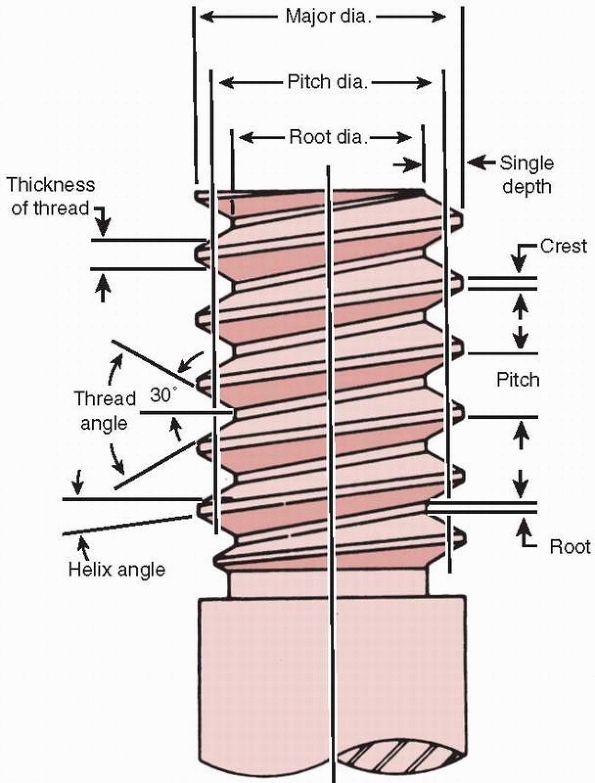
the fixation plate, causing compression between them.¹²³ The basic components of a screw are shown in Figure 1-27.
Because of its function, the screw head and shaft should be free to
turn in the plate; otherwise the compressive force generated may be
limited. (This doesn’t apply to screws that are designed to be threaded
into the plate holes in locking plates.) One common problem is that
sometimes threads are tapped into both bone components. The bone
component in which the screw head will rest should be drilled oversize
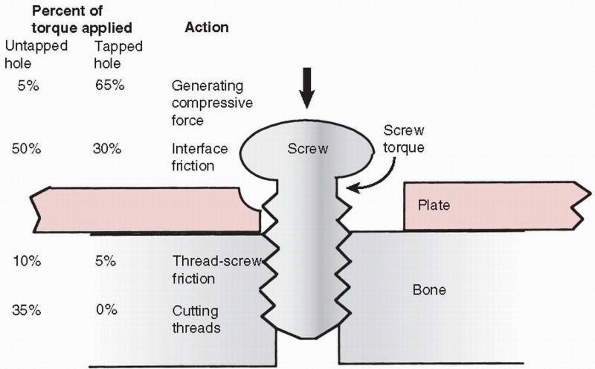
to allow the shaft of the screw to turn freely. Tapping is necessary in
cortical bone so that the torque applied by the surgeon is converted
into compression instead of cutting threads and overcoming friction
between the screw thread and bone (F_t in Figure 1-26) that it is being driven into (Fig. 1-28).⁷⁵
At the same time, self-tapping screws are available and, when used,
those with multiple cutting flutes at the tip of the screw appeared to
be the easiest to insert and had greater holding power.¹⁶⁵
With cancellous bone, as discussed later, tapping is less advantageous,
unless the bone is very dense. One common problem during screw
placement is shear failure of the screw, typically the head twisting
off leaving the shaft embedded in bone and difficult to remove. This
can occur especially when using smaller (less than 4 mm diameter)
screws in dense bone, especially without tapping. The stiffness and
strength of a screw are related to the 4th power of its diameter (the
effect of moment of inertia, for screws of the same material). A 6-mm
diameter screw is approximately 5 times as stiff as a 3-mm diameter
screw and 16 times as resistant to shear failure by over-torquing the
screw during insertion.

FIGURE 1-26
A screw is a mechanical device that converts torque into compression
between objects. The screw thread is actually an inclined plane that
slowly pulls the objects it is embedded into together. For this reason,
the head and screw shaft in one part must be free to rotate. If this
part of the screw is threaded into the hole of the first part (for
example, the plate) it will not allow the surfaces to compress (Fn,
normal or compressive force acting against the screw head; Ft,
tangential or frictional force acting along the screw thread; Fz,
resultant of the two forces, α, angle of the screw thread. The smaller
the angle α [finer thread] the lower the frictional force).

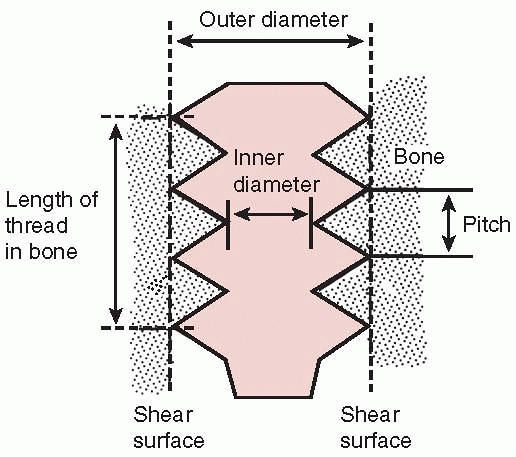
FIGURE 1-27
Nomenclature of screws. The root diameter is the inner diameter of the
screw and the pitch defines the distance between threads.

FIGURE 1-28
Schematic diagram showing the approximate distribution of torque acting
on screw placed into cortical bone. With a pretapped hole, about 65% of
the applied torque goes to produce compression and 35% to overcome the
friction associated with driving the screw. When the hole is not
tapped, only about 5% of the torque is used to produce compression, the
rest going to overcome friction and to cut threads in bone. These
observations do not apply in cancellous bone.

Screw Pullout

Particularly in cancellous bone, the maximum force that
a screw can withstand along its axis, the pullout force, depends upon
the size of the screw and the density of the bone it is placed into. As
shown in Figure 1-29, when the force acting on
the screw exceeds its pullout strength, the screw will pull or shear
out of the hole, carrying the sheared bone within its threads, because
it is usually the bone that fails and not the screw. The pullout force
increases with larger screw diameter, a longer embedded length of screw
shaft, and greater density of the bone it is placed into.³³,⁴⁵,⁵⁸,¹³⁴
The diameter and length of the embedded screw can be thought of as
defining the outer surface of a cylinder along which the screw shears.
Given the maximum stress that bone of a particular density can
withstand, increasing the surface area of the screw cylinder increases
the pullout force (because force = stress × area over which it acts).
To enhance screw purchase, consider embedding the largest diameter
screw possible into bone of the greatest density over as long a
purchase length as possible.³³,⁴⁵ Pullout strength also increases significantly if the screw is placed through both bone cortices.

In cancellous bone, screw pullout becomes a more significant

P.20

problem because the porosity of cancellous bone reduces its density and therefore its shear strength.¹⁴⁸
Hole preparation, specifically drilling but not tapping, improves the
pullout strength of screws placed into cancellous bone (such as pedicle
screws in the vertebral body).³³ The reason that tapping reduces strength in cancellous bone, as shown in Figure 1-30,
is that running the tap in and out of the hole removes bone,
effectively increasing the diameter of the hole and reducing the amount
of bone material that interacts with the screw threads. Tapping has
more effect as bone density decreases and can reduce the pullout
strength from 10% to as much as 30%. It should also be noted that the
findings of studies related to pullout strength relate to the time
immediately after insertion. As the bone heals, it also remodels around
the screw, possibly doubling its initial pullout strength.¹³⁴

FIGURE 1-29
The factors that determine the pullout strength of a screw are its
outer diameter and length of engagement (this defines the dimensions of
a cylinder of bone that is carried in the threads and is sheared out as
the screw is pulled out of bone) and the shear strength of bone at the
screw/bone interface, which is directly related to its density. A finer
pitch screw produces a small gain in purchase.³³

Screw Breakage by Cyclic Loading

A mechanism exists through which cortical screws can fail because of cyclic bending, shown in Figure 1-31.
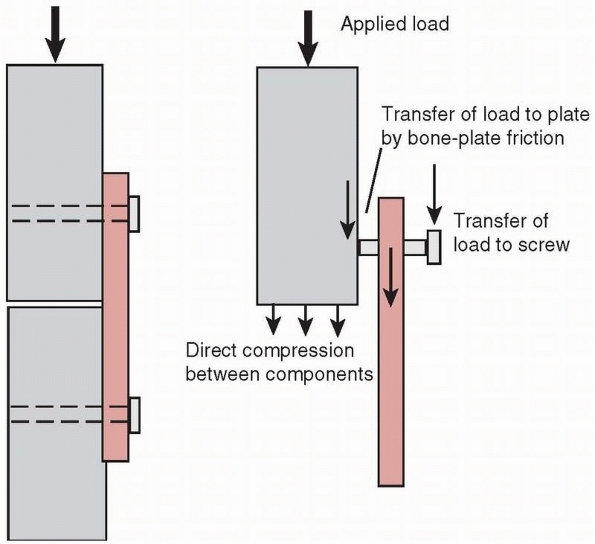
This mode of loading could occur during functional use; for example,
with a dynamic compression plate (DCP) but not a locking plate. The
screw should be tightened against the DCP plate to the maximum extent
possible and the tightening torque effectively transferred to
compressive force between plate and bone (see Fig. 1-28).
The screw holds the plate against bone partly by frictional contact,
which depends on the frictional force generated between the
undersurface of the plate and bone. The frictional force is directly
dependent on the compressive force generated by the screws. If any
sliding occurs between the plate and bone, bending load will be
transferred from the head of the screw into the plate, where
screw-plate contact occurs. Bending loads perpendicular to the axis of
the screw, along with possible stress corrosion and fretting corrosion,
may cause the screws to fail rapidly in fatigue. Zand et al¹⁶⁸
showed that screws tightened against a plate with only 10% to 15% less
force than the maximum possible failed in less than 1000 loading
cycles, by bending fatigue, compared with fully tightened screws that
were able to sustain over 2.5 million loading cycles. Screws that lock
into the plate reduce this problem. Small fragment screws, around 4 mm
outside diameter, can fatigue because their core diameters are small.
The trade-off in use of these devices is choosing a screw with a larger
core diameter and shallower thread to reduce the possibility of
fatigue, or a smaller core diameter and deeper thread to increase
purchase strength in bone.¹¹¹

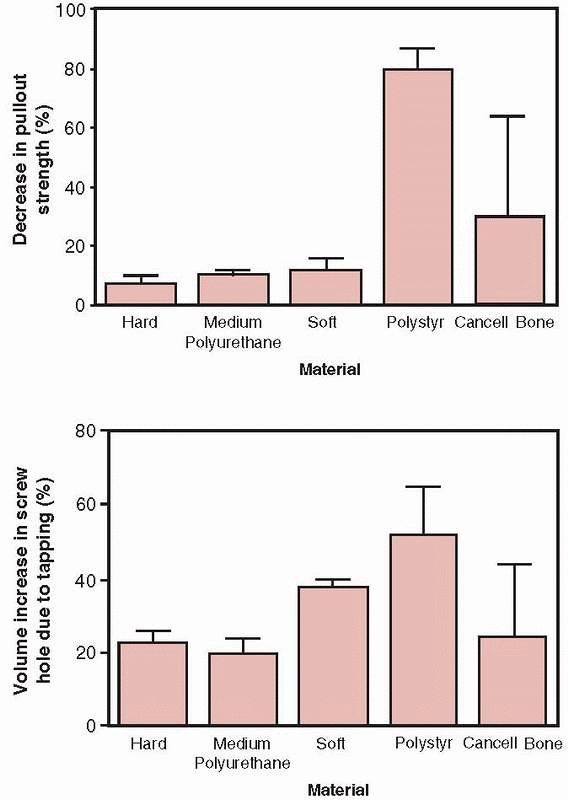
FIGURE 1-30 Top:
The decrease in pullout strength in various types of foam used to test
bone screws demonstrating the percentage decrease in pullout strength
between screws placed into holes that were either drilled only or
drilled and tapped. Bottom: The percentage
increase in volume comparing holes that were drilled only and those
that were drilled and tapped. Tapping in cancellous bone increases hole
volume, which decreases pullout strength.³³

Cannulated screws are commonly used for fixation, having
the significant advantage that they can be precisely guided into
position over a guide wire, which itself may aid in reduction of a
fracture fragment. Nevertheless, drilling precision for the screw or
guide wire is decreased with increasing density of bone, and the use of
longer and smaller diameter drill bits.⁷⁴
Cannulated screws follow the same mechanical principles as solid
screws, however, to create the central hole, material must be removed
from the center of the screw. Manufacturers commonly increase the minor
diameter (the diameter of the screw at the base of the thread) to
accommodate the loss of this material. The same size cannulated screws
usually have less thread depth compared with solid screws. The
result—depending on the screw size—is less pullout strength. For 4-mm
diameter screws, cannulated screws of the same outside diameter had
about 16% less pullout strength.¹⁵¹ Alternatively, to keep the same thread depth, the outer diameter of the screw may be increased.

P.21

FIGURE 1-31
A mechanism for rapid failure of screws in cyclic bending occurs when
the screw has not been tightened sufficiently to keep the plate from
sliding along the bone surface (the plate-bone gap shown here is
exaggerated for clarity). The result is that bending loads are applied
transverse to the long axis of the screw, which in combination with
fretting corrosion caused by the screws rubbing against the plate
results in early failure of the screw.

Breakage of Fracture Fixation Plates

The fracture fixation plate is designed to stabilize a
fracture by driving the ends of the fracture together, compressing
them. This is beneficial to fracture healing because it improves
stability, opening the possibility for primary bone healing with
minimal callus formation, and by enhancing the resistance of the plate
to bending fatigue failure. Observing the cross section of an oval hole
in a dynamic compression fracture plate, Figure 1-32,
shows that one border of the hole actually has an inclined surface.
When the head of the screw displaces downward toward the bone surface,
the screw and the fragment of bone it is attached to slide toward the
center of the plate. This action, which occurs in both fracture
components, causes the fracture surfaces to be driven together² and creates significant compressive forces across the ends of the fracture.³⁷
Compressing the ends of the fracture significantly improves the
stability of the construct and reduces bending and torsional stresses
applied to the plate, increasing its life. Stability is improved
because the bone ends resist bending forces that close the fracture
gap, and torsional loads are resisted by the frictional force and
interlock between the ends of the fracture components. Also, the
fracture gap that must be healed is smaller.

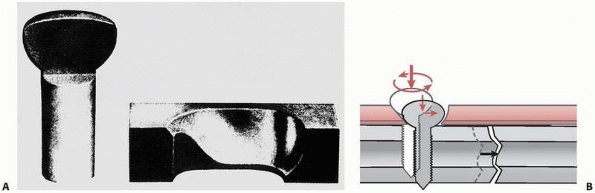
FIGURE 1-32 A. Cross section through the head of a bone screw and the hole in a fracture plate showing the geometry. B.
As the screw is tightened, the head slides down the inclined border of
the plate, which displaces the screw sideways, and therefore the screw
and the bone fragment to which the screw is attached are displaced
toward the opposite fragment.

FIGURE 1-33 Left:
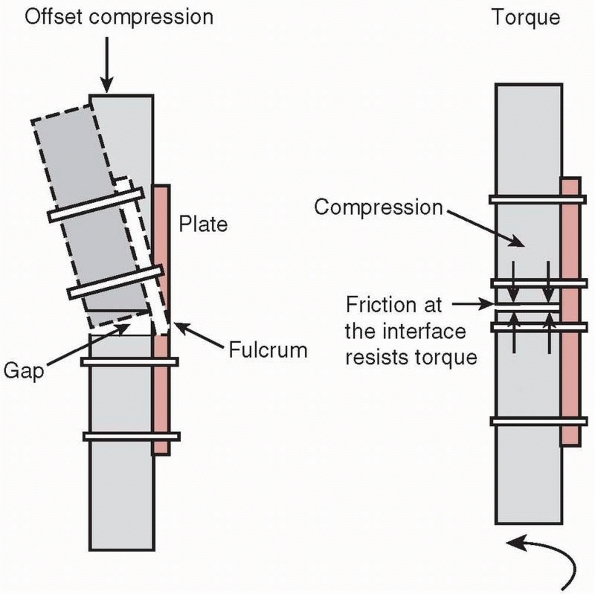
When a gap is left on the cortex opposite that to which the plate is
attached, bending of the plate at the fracture site can cause the plate
to fail rapidly in bending. Right:
Compressing the fracture surfaces not only allows the bone cortices to
resist bending loads but the frictional contact and interdigitation
help resist torsion.

It is important to appreciate that the plate is
vulnerable to bending failure, because plates are thin, relatively easy
to bend (compared to bone), and have low moments of inertia. They are
designed to apply compressive force to the ends of the fracture, and
the stabilized bone can then resist the bending loads applied during
functional use. If a gap is left on the side opposite the plate, Figure 1-33,
the fracture site becomes a fulcrum around which the plate bends under
combined compressive and bending loads such as those which occur during
ambulation (if the compressive force is not located directly down the
tibial

P.22

shaft,
which occurs during heel strike and toe off, then bending loads will be
applied along with the compressive force). Gapping can also occur when
a segment of bone is missing at the fracture site, or if the plate is
not properly contoured during application. Figure 1-34
demonstrates how a flat, noncontoured plate tightened against a flat
bone surface will cause a gap to appear on the opposite cortex.¹¹⁸
This is why a plate should be prebent sufficiently to create an initial
gap between it and the bone surface it will be applied to.⁶⁸,¹¹⁹,¹³⁶
Gapping at the fracture also occurs when the plate is applied to the
predominantly compressive side instead of the tensile side of a long
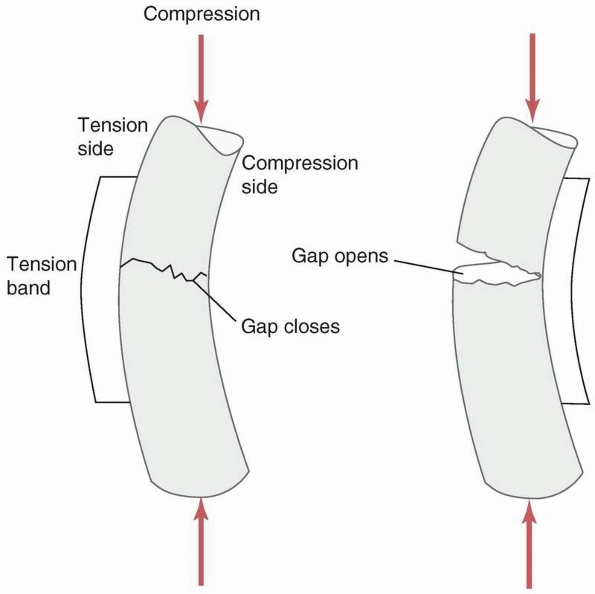
bone during functional loading that causes bending. Figure 1-35 demonstrates that placing the plate on the compressive side will cause a gap to open under load.

FIGURE 1-34
A demonstration of the gapping that occurs on the opposite cortex when
a flat plate is applied to a flat bone surface. Slightly prebending the
plate causes the ends of the opposite cortices to be driven together
when the plate is applied.¹¹⁸

Plate stresses are significantly increased by gapping at the fracture.¹⁴
In comminuted fractures in which it is difficult to approximate the
fracture ends, screws should be placed as close as possible across the
fracture gap to reduce strains in the plate.⁵³
Torsional and bending stiffness of a fracture construct can be
significantly increased, and therefore plate strain reduced, by
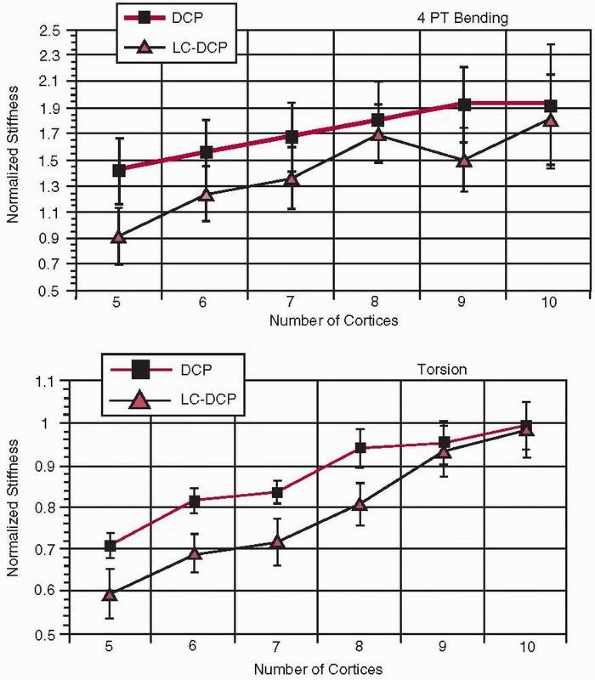
increasing the length of the plate itself¹³³ as well as with several cortices of fixation (i.e., screw-cortex contact). However, as shown in Figure 1-36,
there is an optimum number of cortices, eight for DCP plates and nine
for LC-DCP plates, beyond which there is little additional gain in
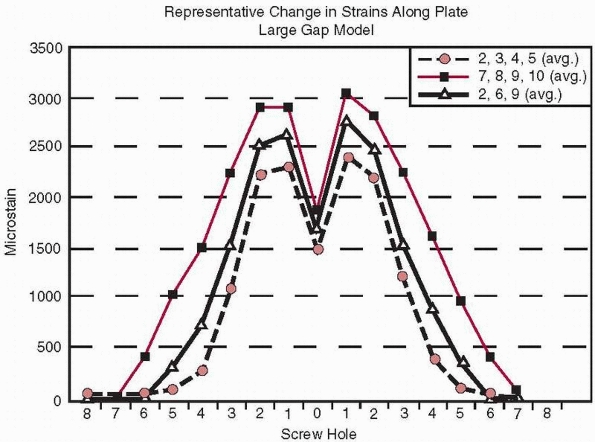
torsional stiffness⁵⁴. Figure 1-37
shows several interesting aspects related to plate fixation with
screws. First, plate strains are highest at the two holes adjacent to
the fracture gap and become very small five holes away. Second, this
occurs regardless of whether the screws were placed near the fracture
(locations 2, 3, 4, and 5), far from the fracture (locations 7, 8, 9,
and 10), or were mixed (locations 2, 6, and 9).⁵³ This data also indicates that not all holes of the plate need to be filled with screws to provide similar fixation stiffness.

FIGURE 1-35
The application of a plate on the compressive as opposed to the tensile
side of a bone subjected to bending causes a gap to open on the
opposite side of the plate during functional loading.

A significant recent development in plate design is the locking or LISS (less invasive stabilization system) plate,⁶⁰ also called the noncontact plate or internal fixator,⁸³
in which the screw head has a machine thread, separate from the bone
thread, which locks it to the plate. The screws and plate form a rigid
connection. In addition, the screws have been designed with a finer
thread for unicortical fixation.⁵³
The LISS plate functions differently biomechanically from the dynamic
compression plate (DCP). The DCP plate is compressed against the bone
fragments by the screws and requires bone to plate contact to produce a
stable fracture construct. Buttressing of the opposite cortex is
important in maintaining fracture stability and reducing plate stresses
with the DCP plate. Bending loads applied to the screws in the
nonlocking DCP plate caused the screws to rotate within the plate
resulting in fracture fragment motion, higher plate stresses, and
reduced stability at the fracture site.

The LISS plate acts conceptually like an external fixator,⁶⁰
in which the pins (screws) are rigidly connected to the side bar (the
plate) and bone to fixator contact is reduced in the low contact plate
version. This produces less interference with the biological processes
of fracture healing, especially helping to preserve the blood supply
near the fracture site. Also, the LISS plate provides more stability in
comminuted fractures¹⁴² in which
cortical buttressing and compression are difficult to achieve and
fracture mechanical stability occurs mainly from the hardware.⁵⁰
LISS plates do not allow the screws to be directed obliquely, except
when specifically designed into the implant, and do not generally
develop interfragmentary compression at the fracture site. Bending
loads applied to the screws from bone are resisted by the locking
interface between the threads in the screw head and the threads in the
plate. Therefore, these plates are not as dependent on cortical
buttressing for stability as the DCP plate. Dynamic fatigue testing has
shown that LISS plates have fatigue strengths similar to other systems
and are able to support loads comparable to 1 bodyweight for 2 million
cycles, which should be sufficient for normal fracture healing. Because

P.23

screw
pullout strength is related directly to the length of screw purchase in
bone cortex, the unicortical screws used in some systems have lower
pullout strength than bicortical screws. More screws must be used to
compensate for the inherent lower pullout strength of the unicortical
screw. As with other systems, the LISS plates have mechanical
sensitivities. For example, accurate placement of the locking screws is
important. As Figure 1-38
shows, angulation of the screw causes incomplete engagement and,
therefore, lower mechanical stability of the construct. In fact,
comparatively, the bending stability of a 4.5-mm LISS plate was reduced
to 63% and 31%, respectively, caused by a 5- or 10-degree misalignment
of the locking screws in the plate.⁸¹

FIGURE 1-36 Relative stiffness of a plate-bone construct in (top) torsion and (bottom)
bending as a function of the number of cortices through which screws
have been placed (DCP, dynamic compression plate, LC-DCP, limited
contact dynamic compression plate).⁵⁴

FIGURE 1-37 Distribution of strain (measured in microstrain or strain × 10^-6)
at various locations along a plate regardless of placement of the
screws in different locations (holes 2, 3, 45), (holes 7, 8, 9, 10), or
holes (2, 6, 9).⁵³

P.24

FIGURE 1-38 A demonstration of the importance of accurate placement of locking screws into the plate.⁸¹

Plate Failure through a Screw Hole

Many plates are long with multiple screw holes to
provide flexibility of fixation of bone fractures with complex
geometries. It is not necessary to place screws in every hole in the
plate,⁴⁶ but the effects of screw
placement on fixation stiffness should be understood. The screw hole
will be an area of elevated stresses on the plate, unless the plate is
made thicker near the holes to compensate, as is the case with some
plates. Placing the plate so that an empty screw hole is located over
the fracture will significantly increase the potential for fatigue
fracture of the plate. The plate material around the holes will have
higher material stresses than occurs in the solid regions of the plate.
Around the holes, the force acts through a smaller cross-sectional
area, so the material stresses must be higher. A second consideration
related to multihole plates is that separating the screws so that there
is a greater distance between them across the fracture site results in
lower stiffness of the plate-fracture construct. As with any beam
(plate), the greater the distance between the supports (screws), the
greater the bending displacement and the higher the stresses will be
for the same applied load. It is best to avoid placing screw holes over
or near the fracture site and it is beneficial, in terms of improving
fixation stiffness, to place screws as close together across the
fracture site as possible.

Fully Threaded Lag Screws

The lag screw is a very effective device for generating
large compressive forces across fracture fragments, and these forces
are applied directly across the fracture site. The head and upper part
of the shaft of the screw must be allowed to glide in one fracture
component so that it pulls the other fracture component towards it to
create compression across the two. As shown in Figure 1-39,
a fully threaded lag screw blocks the gliding action between the two
components. Comparing the compressive forces across the fracture site
using fully and partly threaded lag screws demonstrated that the
average compressive force at the opposite cortex (i.e., the force in
the screw itself) was about 50% greater when a partly threaded screw
was used.⁸⁶

Femoral Splitting as a Result of IM Rod Insertion

Insertion of an intramedullary (IM) rod into the femur
can lead to difficulties because the femur has a significant anterior
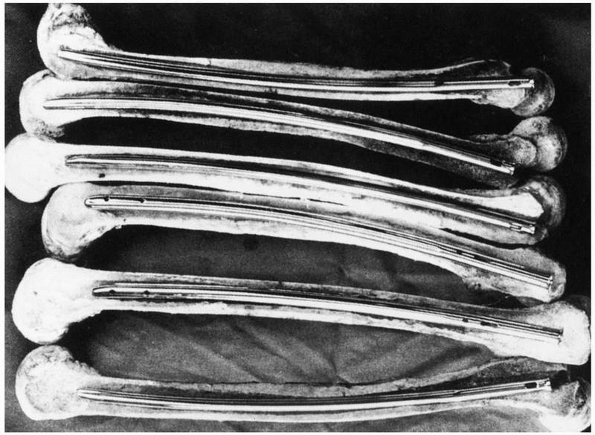
curvature,¹⁶⁹ shown in Figure 1-40.
Current femoral nails have radii of curvature that range from 186 to
300 cm, compared with the average for a large sample of femora, which
was 120 +/- 36 cm. Therefore, current femoral nails are considerably
straighter than the femora they are inserted into.⁴⁹
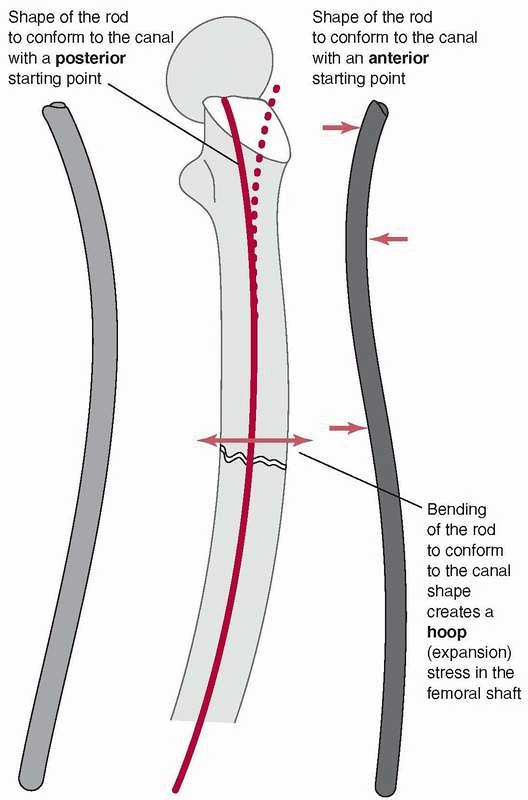
The rod, which also has a curved shape to accommodate the femoral bow,
must conform to the curvature of the femur as insertion progresses.
Placing a rod, which is essentially a steel curved spring, down the
femoral canal causes the rod to bend, because the femur is generally
much stiffer than the rod, Figure 1-41. In fact, the nail must conform not only to an anterior-posterior

P.25

bow but also canal curvature medially and laterally.⁵¹ Figure 1-42
demonstrates that rod contact with the internal surfaces of the femur
generates forces which resist insertion. These rodfemur contact forces,
directed perpendicular to the surface of the medullary canal cause the
femur to expand and will result in splitting if they become too large.⁸⁰

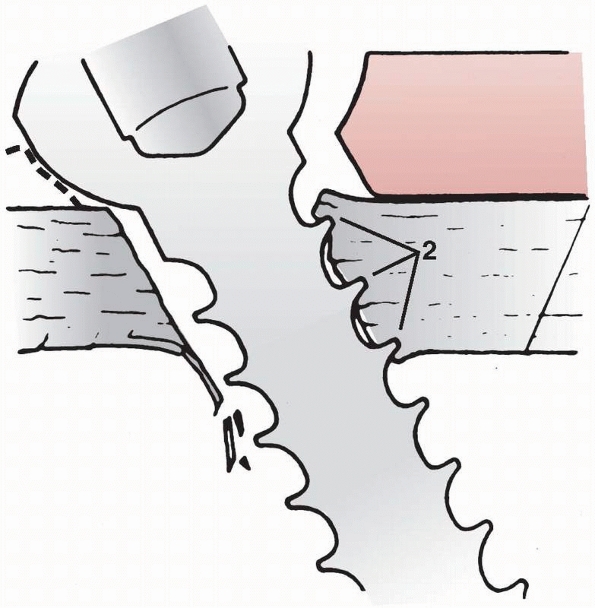
FIGURE 1-39
Using a fully threaded lag screw causes the threads to engage in bone
on both sides of the fracture. This inhibits the screw from compressing
the bone fragments together.⁸⁶

FIGURE 1-40 Cross sections of various femora demonstrate the curvature that an IM rod must conform to when it is fully inserted.¹⁶⁹

FIGURE 1-41
Mismatch of the curvature between the IM rod and the medullary canal
results in bending stresses that could cause splitting of the femur
during insertion.⁸⁰

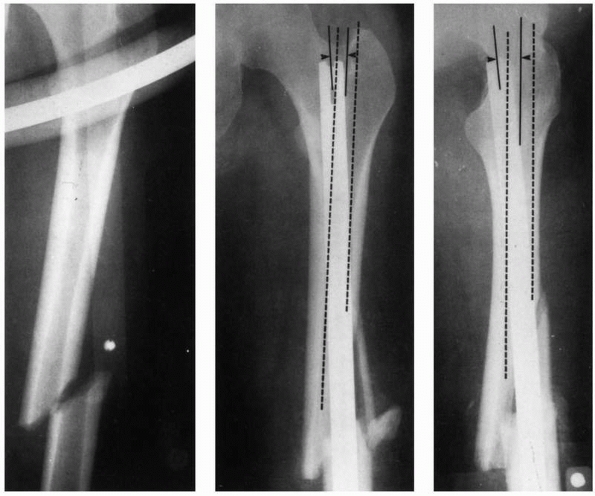
The factors that govern the amount of bending of the rod
during insertion and the resulting internal forces acting within the
femur are the proximal starting hole position, the length of the
proximal fragment, the initial curvature of the IM rod compared with
the curvature of the femur, and the rod bending stiffness. Stiffnesses
of rods can vary considerably.¹³¹ Figure 1-42 demonstrates examples in which rod proximal starting hole position resulted in femoral splitting during rod insertion.⁸⁰ Some newer IM nails employ a valgus bend to be used with a femoral trochanteric entry portal.¹²⁰
The optimal entry point for retrograde nailing, used selectively when
antegrade nailing is not possible, was found to be about 1.2 cm
anterior to the femoral origin of the posterior cruciate ligament and
at the midpoint of the intracondylar sulcus.⁹¹

IM Rod and Locking Screw Breakage

Fractures of IM rods and locking screws occur
occasionally during healing. The most demanding mechanical situation
for IM rod fixation of the femur or tibia occurs when the fracture is
very distal. Figure 1-43 compares the forces
acting on idealized femora with more proximal and more distal
fractures. For a specific location of the external load (muscle load or
body weight), the more distal fracture results in a longer moment arm
(the perpendicular distance from the load to the fracture site)
creating a greater moment, and therefore higher stresses in the rod.
The highest stresses in the rod occur near the fracture site. With a
distal fracture, in addition to the greater moment, the locking
holes—which are significant stress risers—are usually located just
distal to the fracture site. It has been shown that the maximum
stresses acting in the rod increase rapidly once the distance between
the fracture and the most superior of the distal screw holes is reduced
to less than about 4 cm.²⁸ Cyclic
loading of nails used to fixed distal fractures, with peak loading of
about 1 times bodyweight, confirm that titanium alloy nails can survive
more than 1 million loading cycles when the more proximal of the distal
locking screws is more than 3 cm from the fracture site.⁷
In addition, placing the distal locking screws can be difficult because
they must be inserted freehand under fluoroscopic guidance. Sometimes
the corner of the screw hole of the rod can be nicked by the drill or
while driving the screw, creating an additional stress riser that can
accentuate the fatigue process. Awareness of these potential problems
has led to design changes such as closing the proximal section of the
rod, increasing material thickness around the screw holes, and cold
forming, which increases the strength of the rod material.

Screw bending and breakage can also occur. When distal
screws are placed into bone with relatively low bone density, the screw
is supported mostly by the cortices. The distal end of the femur widens
rapidly (Fig. 1-44), so the unsupported length
of the screw between the cortices can be quite variable. For the same
diameter and material, the stiffness and strength of a screw subjected
to bending decreases with the third power of its unsupported length
(the distance between cortices, assuming no support from the trabecular
bone). If the unsupported length of one screw is twice as long as that
of another, and assuming that the trabecular bone does not contribute
to support of the screw, one can expect the stiffness and strength of
the screw with the longer unsupported length to be 8 times less than
that of the screw with the shorter length between cortical supports,
and therefore the deformation will be 8 times greater under the same
load. This does create a tradeoff in fixation of

P.26

these
fractures with respect to screw placement. If the screws are too close
to the fracture, the stresses in the rod increase, while if they are
located within the flair of the metaphysis, with poor trabecular bone,
their unsupported length increases, decreasing stiffness and strength.
The fatigue life of the distal locking screws is directly related to
the diameter of the root of the thread and the resulting moment of
inertia, so it has been proposed to remove the threads to increase
fatigue life by 10 to 100 times.⁷³

FIGURE 1-42
The starting position selected for rod entry into the medullary canal
affects the degree to which it must bend and the internal forces
generated in the femur. A starting position offset from the axis of the
medullary canal, coupled with a stiff rod and a longer proximal segment
that requires the rod to bend more during insertion, generate higher
insertion forces and internal femoral forces. In this example of a
midshaft femoral fracture (left), the starting hole was selected medial relative to the axis of the medullary canal (middle) and posterior (right).
The medullary canal is outlined in dashed lines. Therefore the rod must
bend both medially and posteriorly as it is inserted into the canal and
has created internal stresses which have split the distal end of the
femur.⁸⁰

FIGURE 1-43 If the same force acts on IM rods placed in femora with more proximal (left) or more distal (right)
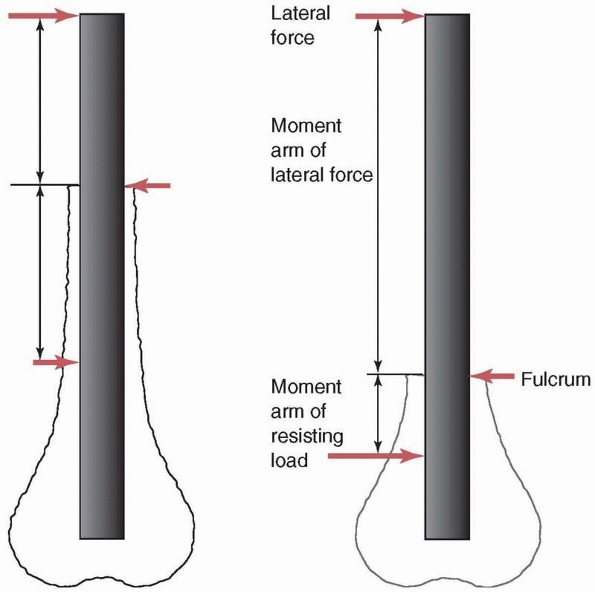
fractures, the moment arm of the force will be longer in the case of
the more distal fracture and therefore the moment acting at the
fracture site on the implant will be larger. For the more distal
fracture, the high stress region close to the fracture site is also
significantly closer to the distal locking screw holes which are
significant stress risers.

Loosening of External Fixator Pins

Loosening of fixator pins in bone is thought to result
from several causes. The shape of the end of the pin itself, because it
is self-tapping, can affect the local heat generated in bone during
insertion, potentially causing thermal necrosis around the pin hole
site,¹⁶⁰ along with bone microcracking. In addition, high

P.27

local stresses can occur in the pins and bone if the hole through which the pin is inserted is undersized.⁷⁸ A third mechanism, Figure 1-45,
is micromotion, which induces bone resorption at the pin/bone interface
if the pin is a loose fit in the hole. To reduce these problems, slight
undersizing of the bone hole by about 0.1 mm in diameter has been
advocated. If the bone hole is undersized by 0.3 mm in diameter, the
yield strength of bone may be exceeded when the pin is inserted.¹¹⁸

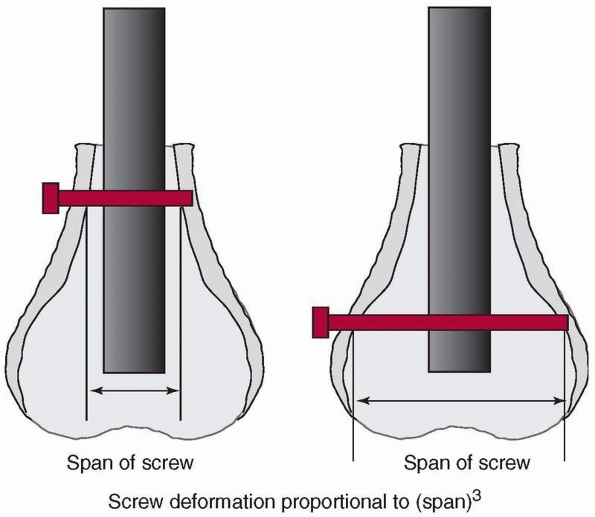FIGURE 1-44
Because the distal end of the femur flares rapidly, the length of the
locking screw required to crosslock the rod can be quite variable. If
the screw is not well supported by trabecular bone but mainly by
cortex, then its stiffness and strength decrease with the 3rd power of
its length between cortices. If the screw length doubles, the
deformation of the screw under the same load increases by a factor of 8.

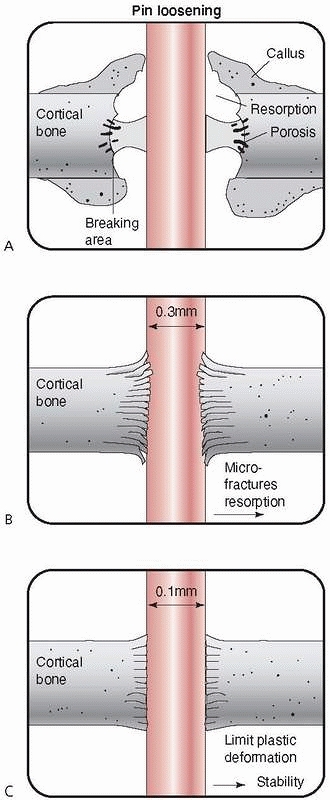FIGURE 1-45
A proposed mechanism for loosening of external fixation pins involves
under- or oversizing the diameter of the pin relative to the bone hole.
A. If the pin and bone hole are the same diameter, micromotion can occur with bone resorption. B. If the pin is more than 0.3 mm smaller in diameter than the hole in bone, microfracture may occur during insertion. C.
If the bone hole diameter is about 0.1 mm smaller than the pin
diameter, the bone is prestressed but does not fracture, micromotion is
eliminated, and pin stability is maintained.¹¹⁸

Excessively Flexible External Fixation

An external fixator is an assembly of pins attached to
bone fragments, along with clamps and sidebars that couple the pins.
This assembly allows considerable variation in construction of a frame
to accommodate the fracture. The optimal stiffness of a fixator is not
specifically known. The stiffness necessary to stabilize the fracture
and induce healing changes as the fracture consolidates. It must be
rigid enough to initially support the forces applied by the patient
during ambulation without causing malalignment of the fracture. On the
other hand, it should not be so stiff that the fracture is shielded
from the stresses required to stimulate healing. Some basic mechanical
guidelines in the construction of the frame, explained below, will
ensure that frames are adequately constructed for the loads they are
subjected to. Figure 1-46 demonstrates that
when the diameter of a pin or sidebar increases, its stiffness and
strength increase to the 4th power of the relative change in diameter
(actually the ratio of the larger to the smaller diameter). As its
length (distance between bone surface and sidebar) decreases, stiffness
and strength increase to the 3rd power of the length change. This
principle also holds also for the pins spanning the fracture, which
affect the unsupported length of the sidebar across the fracture.

In construction of a frame, it is beneficial to decrease
the sidebar to bone distance, which decreases the unsupported lengths
of the pins, increases the pin diameter, and decreases the distance
between the pins which span the fracture—for example, increasing the
number of pins applied also increases frame stiffness. In terms of
actual effects, for example in bending, doubling the sidebar distance
from bone decreases frame stiffness by about 67%, doubling the
separation distance of the pins across the fracture decreases stiffness
by 50%, and decreasing pin diameter by 1 mm (from 6 to 5 mm, for
example) also decreases frame stiffness by about 50%.¹⁵²
Using a partly threaded pin and burying the pin thread completely
within the cortex enhances the stiffness of the pin, because the
smaller diameter of the root of the pin thread is not exposed. Also,
using hydroxyapatite coated external fixation pins to enhance the
screw-bone interface¹¹⁷ can be a good option.

The comments above pertain to uniplane fixators, which
are constructed to resist the major loads, axial compression, and
anterior-posterior bending, acting on a long bone such as the tibia
during walking, with the sidebar usually aligned with the
anterior-posterior plane. To resist torsion and out-of-plane
(medial-lateral) bending, the fixator can be assembled with additional
pins and sidebars in other planes. A comparison of the relative
stiffnesses of different fixator assemblies is given in Figure 1-47.
The unilateral half pin frame with sidebars mounted at right angles
provides the greatest overall resistance to bending, compression, and
torsional loads.²⁰ Hybrid fixation
devices have adopted components of both unilateral bar fixators and
ring fixators with wire transfixing pins. Both axial compression and
torsional stiffnesses have been found to increase significantly with
increases in the number and diameter of the transfixing wires, and
pretensioning the wires.³¹ More
anterior placement of wires, or addition of an anteromedial halfpin
have been found to increase anterior-posterior bending stiffness.⁶³ Testing of several different configurations (see Figure 1-48)
showed that the box type (two rings above and two below the fracture,
along with anterior half pins, two connecting rods and a unilateral
bar) was the stiffest configuration, compared with a unilateral frame
alone or a unilateral frame with rings only proximal to the fracture
site. The addition of an anterior half pin significantly increased
fixation stiffness.¹²⁸

P.28

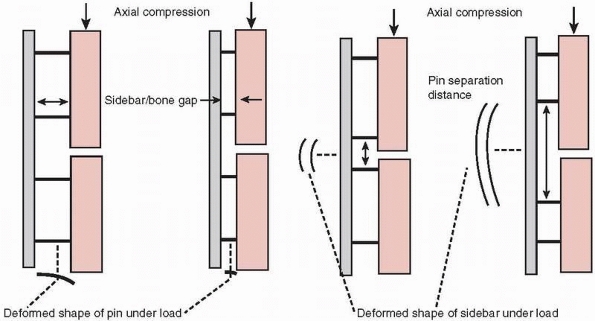FIGURE 1-46
To produce more rigidity in construction of an external fixator, the
basic principles that should be considered are that for pin and rod
type sidebars, stiffness increases with the 4th power of the
cross-sectional area (the moment of inertia, Fig. 1-7) and decreases with the 3rd power of their span or unsupported length (Fig. 1-44).
This explains why it is beneficial to decrease sidebar to bone
distance, increase pin diameter, place pins as close together across
the fracture site, and use larger diameter or multiple sidebars in
frame construction.⁷⁷,¹⁵²

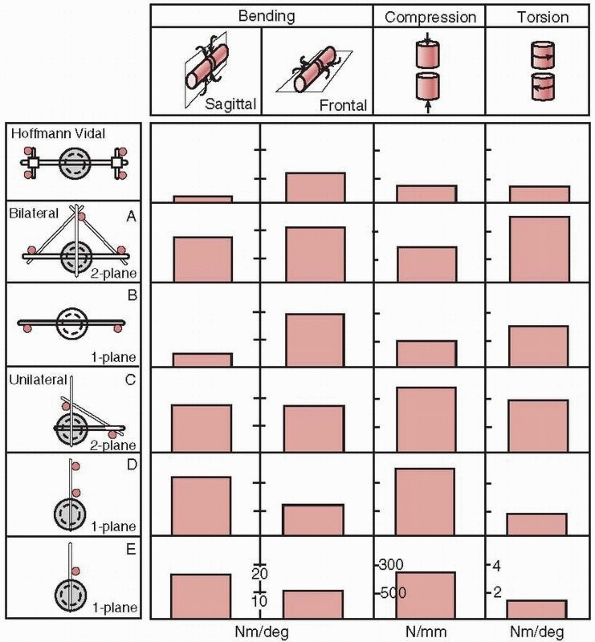FIGURE 1-47
A comparison of the bending, compression, and torsional stiffnesses of
different external fixation constructs for multiplane load resistance.²⁰

P.29

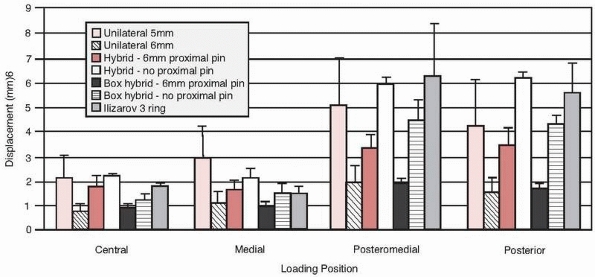FIGURE 1-48
A comparison of displacement of the proximal fragment in a simulated
tibia fracture under 100N load with various unilateral and hybrid
external fixators (the box type uses both a large unilateral frame
connecting bar and two smaller diameter connecting rods).¹²⁸

Fixation in Osteoporotic Bone

Because the attachment strength of a fixation device to
bone, a screw for example, is directly related to the local bone
density, and because a dominant mechanical characteristic of
osteoporotic bone is low density, several strategies can be used when
osteoporotic bone is encountered. These include cortical buttressing by
impaction; wide buttressing, which spreads the load over a larger
surface area; long splintage; improved anchoring; and increasing the
local bone density by injection of, for example, hydroyapatite or
methylmethacrylate, see Figure 1-49.⁷¹
Impaction strategies can be applied in fractures of the distal radius,
femoral neck, and lumbar vertebrae. The dynamic hip screw is an example
of a device which allows controlled impaction of the fracture of the
femoral neck. An angled blade plate applied to supracondylar femur
fractures, as compared with a condylar screw, provides wider
buttressing—that is, a larger surface area of contact with bone. The
rafter plate, which permits placement of numerous cancellous screws for
tibial plateau fractures, is another example of the application of this
principle.²⁵ Long splinting with a
longer, more flexible plate has been applied in humerus fractures, and
the interlocked intramedullary rod is a second example of long
splinting. Enhanced anchoring of pedicle screws using augmenting
laminar hooks is an example of augmentation of anchoring.¹⁷
The locking plate, in which the screws are threaded into the plate and
fixed so they cannot rotate, can be useful in stabilizing osteoporotic
fractures when cortical buttressing is not practical because of low
bone density and the fixation hardware must support most of the load.
Hydroxyapatite coated external fixation pins have been shown to enhance
the screw-bone interface.¹¹⁷ Interlocking

P.30

screws, in which a standard screw has a 45-degree hole drilled into the
shaft to accept an interlocking pin, can be used to reduce screw
backout.¹⁰⁷

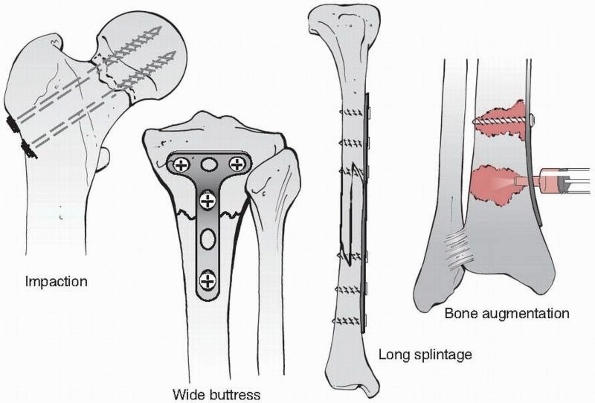FIGURE 1-49
Some basic strategies to augment fixation strength in osteoporotic bone
include impaction of the fracture components using a device that allows
sliding, buttressing with a wide plate, increasing the plate length,
and augmenting the bone locally by injection of methylmethacrylate or a
calcium phosphate cement.⁷¹

Enhancement of local bone density using either PMMA or,
more recently, absorbable hydroxyapatite cements has been studied,
particularly in relation to fixation of femoral and vertebral
osteoporotic fractures. PMMA injection has been widely employed in
vertebroplasty through a transpedicular approach⁹⁹
and has been shown to restore the stiffness of fractured vertebrae to
that of intact vertebrae. Biomechanical studies have shown
significantly improved strength of the fixation of femoral neck
fractures, up to 170%,¹⁴⁷ and
similar findings, including decreased shortening and greater stability
were noted when hydroxyapatite cement was applied to unstable
three-part intertrochanteric fractures fixed with a dynamic hip screw.⁵²
Calcium phosphate cements used in vertebroplasty instead of PMMA also
restored the stiffness of fractured vertebrae to intact levels.¹⁰²
Calcium phosphate cement injection into the pedicle has been shown to
improve the bending stiffness of pedicle screws by up to 125%.¹⁸

Biomechanical Aspects of Fracture Fixation in Specific Locations

In the previous discussion, common problems such as
screw pullout and plate breakage common to fracture fixation mainly in
the long bones were discussed. In this section, the focus is placed on
specific challenging problems in fixation, including the femoral neck,
tibial plateau, pelvis, and spine.

Fixation in the Proximal Femur

Fixation of fractures of the proximal femur is
particularly challenging because the compressive force acting through
the femoral head can range from 4 to 8 times body weight during normal
activities.¹²¹ This force acts
through a significant moment arm (the length of the femoral neck),
which causes large bending loads on the fixation hardware. In addition,
many of these fractures occur in the elderly, who are likely to have
trabecular bone of low density and poor mechanical quality.¹⁰⁰ Also, it is generally not possible to gain screw purchase in the cortical bone of the femoral head.

The major force acting in, for example, a basicervical
fracture of the femoral neck, fixed with a sliding hip screw is the
joint reaction force through the femoral head, which derives from body
weight and forces generated by muscle action during ambulation. The
joint reaction force can be divided into two components. One (Fig. 1-50)
is perpendicular to the axis of the sliding screw and causes shearing
of the fracture surfaces along the fracture line, which results in
inferior displacement and varus angulation of the femoral head, and
increases the resistance of the screw to sliding. The other is parallel
to the screw, driving the surfaces together and enhancing stability by
frictional and mechanical interlocking of the fracture. Therefore, the
aim of femoral neck fixation systems is to utilize the component of the
joint force parallel to the femoral neck to encourage the fracture
surfaces to slide together. This is the basic principle behind
selection of a higher angle hip screw when possible.

When using the compression (or sliding) hip screw, or a
nail with a sliding lag screw, it is important to ensure that the screw
can slide freely in the barrel of the side plate or the hole in the
nail. The following comments related to sliding hip screw devices apply
as well to nail/lag screw constructs. When screw sliding occurs, the
screw is supported by the barrel against inferior bending of the
femoral head because the construct is buttressed by fracture
interdigitation. Adherence to two basic mechanical principles will
enhance the ability of the screw to slide in the bore of the side plate
or nail. As mentioned above, the higher angle hip screw is more
effective at accommodating sliding. Also, the screw should be engaged
as deeply as possible within the barrel. For the same force acting at
the femoral end of the screw, the internal force where the screw
contacts the barrel is increased if less of the screw shaft remains in
the barrel. This occurs because the moment (bending load) caused by the
force transverse to the axis of the screw (Fh in Fig. 1-51)
(at the femoral head) acts over a longer moment arm or perpendicular
distance, Le (force X perpendicular distance to the edge of the barrel,
which is the fulcrum). The balancing moment arm, Lb, is shorter because
less of the screw remains in the barrel. Because Fh acts over a longer
moment arm while Fe acts over a shorter moment arm, Fb increases. The
internal force, Fb, where the screw contacts the barrel causes a
greater frictional resistance force, which requires more force to
overcome to permit sliding.⁹³
Sliding hip screws with either two- or four-hole side plates appear to
provide equivalent resistance to physiologic compressive loading.¹¹⁰

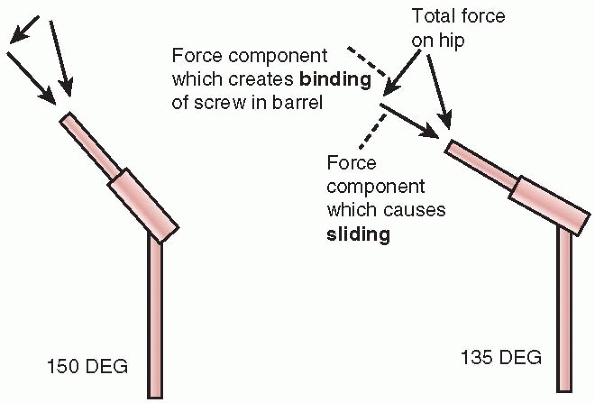FIGURE 1-50
The joint reaction force in the femoral head can be divided into two
major components. The one parallel of the axis of the femoral neck
produces sliding and impaction of the fracture components and the
other, transverse to the femoral neck, causes the screw component of
the femoral hip screw to bind, resisting sliding. The higher-angle hip
screw has a screw axis more closely aligned with the joint reaction
force so the force component that produces sliding is larger while the
transverse force component resisting sliding is smaller.

Several factors affect the strength of femoral neck
fixation using multiple screws, but the number of screws used (three or
four) is not a significant factor.¹⁵⁵
Factors that do increase the strength of this type of fixation include
a more horizontal fracture line with respect to the long axes of the
screws,⁴⁸ placement of the screws in areas of greater femoral head bone density,¹⁴⁵,¹⁴⁹ fractures with less comminution¹²⁹ and a shorter moment arm for the joint load (shorter distance from the center of the femoral head to the fracture line).¹⁴⁵
However, the most important factor has been found to be the quality of
the reduction because of the importance of cortical buttressing in
reducing fracture displacement.¹⁴³ Under physiological load, several mechanisms of failure of fixation have been observed, see Figure 1-52.

P.31

In some cases the screws bend inferiorly, especially if buttressing of
the fracture surfaces inferior to the screws is not possible because of
comminution of the fracture. The fixation screw heads, if no washers
are used to distribute the screw load against bone, have been found to
pull through cortex near the greater trochanter when the cortex is
thin. Finally, if the screws are not well supported inferiorly where
they cross the fracture, they may rotate inferiorly carrying the
femoral head into a varus orientation.¹⁴⁵ Supporting at least one screw against the inferior cortex may help prevent this from occurring.

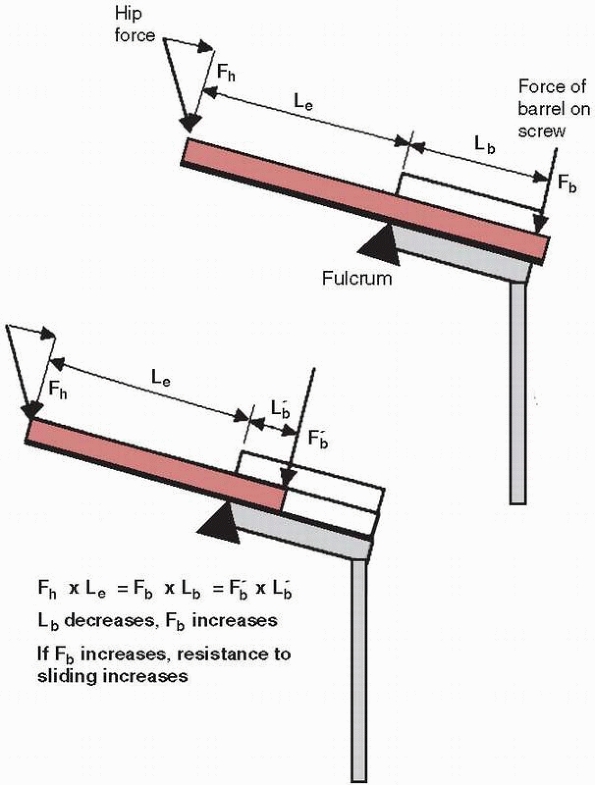FIGURE 1-51
The greater the length of the sliding screw within the barrel, the
lower its resistance to sliding. In this diagram Fh is the component of
the joint reaction force perpendicular to the axis of the screw. The
inferior edge of the proximal end of the barrel is the location of the
fulcrum in bending. An internal force, Fb, from the surface of the
barrel acts against the screw to counteract Fh. For equilibrium, the
moments produced by Fh (Fh × Le) and Fb (Fb × Lb) must be equal. If Lb,
the distance from the point of application of internal force Fb to the
fulcrum, decreases, Fb must increase to produce the same moment. If Fb
is larger, the frictional force and therefore the resistance to screw
sliding will increase. (Le is the length of the screw beyond the
barrel).⁹³

With respect to the biomechanical performance of
different devices, the actual stiffness provided by the sliding hip
screw, the reconstruction nail, and multiple pin constructs are quite
similar, except that the reconstruction nail offers significantly
greater torsional stiffness than the other forms of fixation because of
its tubular shape.⁶⁶,¹³⁰
New techniques applied to proximal fracture fixation include the
femoral locking plate and percutaneous compression plating. In fixation
of the challenging vertical shear fracture of the proximal femur, the
proximal femoral locking plate was found to produce considerably
stiffer constructs than cannulated screws, a dynamic hip screw, or a
dynamic condylar screw.⁶ Percutaneous compression plating has been found to provide adequate bending and torsional stability⁹²
and was equivalent to the trochanteric antegrade nail in fracture site
stability, though it failed at about 2100N (about 3 times body weight)
compared to the antegrade nail at 3200N.⁶⁷

Fixation around the Metaphyseal Region of the Knee

Both supracondylar femur and tibial plateau fractures
are challenging to stabilize because they may involve fixation of
multiple small fragments of primarily cancellous bone. Supracondylar
fixation alternatives that have been compared mechanically include
condylar plates, plates with lag screws across the fracture site, and
blade plates. All devices tested appeared to provide similar construct
stiffnesses. The most important factor identified for plate fixation
was maintaining contact at the cortex opposite that to which the
fixation device was applied. Fixation constructs without cortical
contact were only about 20% as stiff as those with cortical buttressing.⁵⁹,¹⁴⁰
Using a retrograde intramedullary supracondylar nail was found to
produce constructs that were 14% less stiff in axial compression and
17% less stiff in torsion, compared with a fixed angle side plate.¹¹² However, longer nails (36 cm) enhanced fixation stability compared to shorter nails (20 cm).¹⁴⁴
Several newer fixation systems have been described for femoral
supracondylar fracture stabilization. The less invasive stabilization
system (LISS) uses a low-profile plate with monocortical screws
distally which also lock to the plate. LISS plates produced constructs
with more elastic deformation and less subsidence than those with a
condylar screw or buttress plate.¹⁰⁵,¹⁵⁶

Tibial plateau fractures are challenging to stabilize.
Considering patient outcomes, the loss of reduction was related to
patients being more than 60 years old, premature weight bearing,
fracture fragmentation, and severe osteoporosis.⁴ Different methods of fixation include using wires or screws alone, Figure 1-53,
or screws placed through an L- or T-shaped plate, which buttresses the
cortex. Various configurations of wires have been tested²⁴ and show that the stiffness of the construct increases with the number of wires, regardless of their specific orientations. As Figure 1-53 shows, fixation with screws alone requires

P.32

that the screw resist bending forces as the tibial fragment is loaded
distally in compression through the joint. With the addition of a
plate, not only is the load distributed to the plate, but additional
screws can be placed in the stronger cortical bone distal to the
metaphyseal region of the tibia. One disadvantage of a buttress plate
is the additional invasiveness that it requires for installation with
potential compromise of blood supply. Fixation with T plates and screws
showed the greatest resistance to an axial compressive load,⁴⁶ regardless of the specific configuration of the screws.⁸⁴
Investigations of different plate configurations found that for
bicondylar tibial plateau fractures, dual (lateral and medial) side
plating reduced subsidence under axial loading by about 50% compared
with single-sided lateral locking plating.⁷²
For medial plateau fractures, the medial buttress plate, which supports
the load directly, is superior mechanically to a lateral locked plate.¹²⁶
A new alternative is the short proximal tibial nail with multiple
interlocking screws. In combined axial loading, bending and rotation,
the nail provided stability equivalent to that of double plating and
was greater than constructs with a locking plate, external fixator, or
conventional unreamed tibial nail.⁶⁹

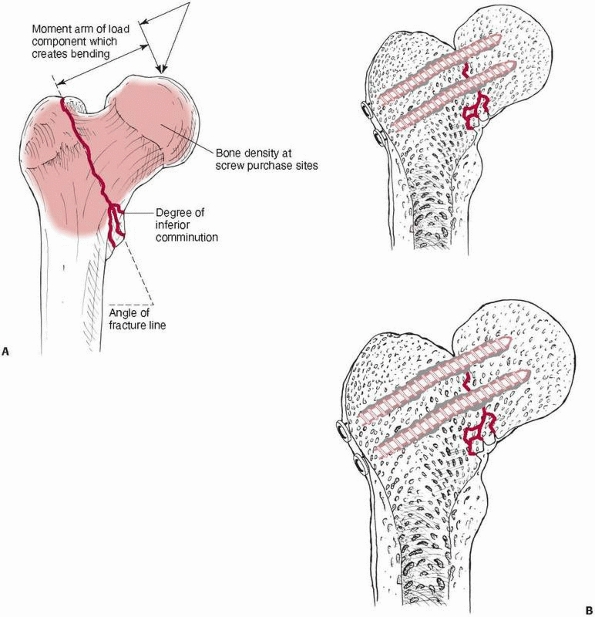FIGURE 1-52 A.
Some factors that decrease the strength of femoral neck fracture
fixation include decreased bone density; a more vertical fracture
surface, which facilitates sliding of the fracture components;
comminution at the inferior cortex, which reduces buttressing against
bending; and a longer moment arm or distance of the center of the
femoral head to the fracture line. B.
Observed mechanisms of failure of femoral neck fixation using screws
include bending of the pins, displacement of the screw heads through
the thin cortex of the greater trochanter, especially if washers are
not used, and rotation of the screws inferiorly through the low density
cancellous bone of the Ward triangle area until they settle against the
inferior cortex.¹⁴⁵

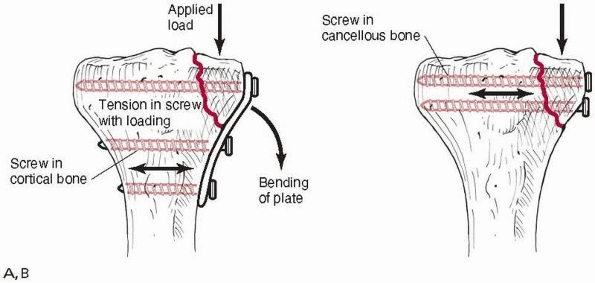FIGURE 1-53 Two alternative methods of fixation of tibial plateau fractures: (A) transverse screws combined with a buttress plate and (B)
transverse screws alone. The buttress plate provides additional support
in bending as the tibial fracture component is loaded in an inferior
direction and allows the screws to engage the thicker, more distal
cortical bone.

P.33

Fixation of the Spine

The halo apparatus is an external fixation device for
cervical spine injuries that are stable in compression. It stabilizes
the injured cervical spine mainly in bending but not in compression.
Factors that affect its mechanical performance include (Fig. 1-54)
the fit of the jacket on the torso and the frictional characteristics
of the lining. High friction linings decrease slip at the vest
lining/torso interface, more rigid vests reduce deflection under loads,
and less flexible superstructures all decrease cervical spine motion at
the injury level. While stiffening the vest enhances its ability to
stabilize the injury, this property must be balanced with enough
flexibility to provide reasonable comfort for the wearer and to
accommodate expansion and contraction of the chest. Because the injured
cervical segment is relatively distant from the vest, small motions of
the vest can result in relatively large displacements at the injury
site.¹¹⁴ A very rigid halo
superstructure attaching the vest to the halo ring may not increase
injury stability if connected to a poorly fitting vest.

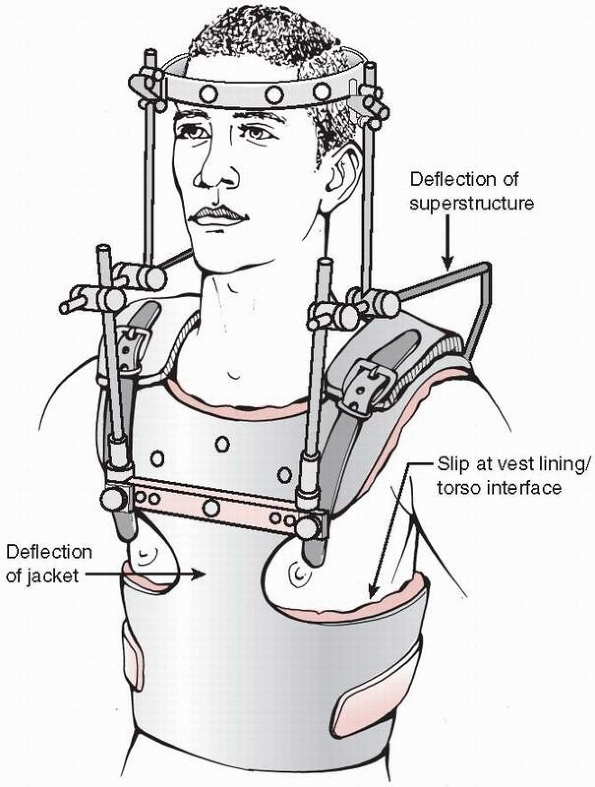FIGURE 1-54
A schematic diagram showing possible sources of deformation in the halo
apparatus. The large distance from the vest to chest contact points to
the cervical injury site results in relatively large motions at the
injury site for small motions of the vest.¹¹⁴

Several methods are available to reconstruct cervical
spine injuries. The major differences between them relate to the
location of the fixation device itself on the vertebra—anterior,
lateral, or posterior—and to the method by which the fixation is
attached to bone. Generally the most rigid fixation is the one with the
longest moment arm from the center of rotation of the injured segment.
For a specific applied moment, say flexion, a posteriorly located
fixation, being located further from the center of rotation, results in
greater rigidity. Figure 1-55 shows the
approximate locations of the centers of rotation at different cervical
spine levels when the posterior elements have been

P.34

disrupted.⁵
After corpectomy, testing has shown that posterior rods provide the
greatest stability, which is unchanged after augmentation with an
anterior plate, while anterior plating alone offers the least stability.¹⁴⁶
Similarly, another test showed that after corpectomy, sagittal plane
motion was most rigid after supplementation with lateral mass plates,
less rigid with an anterior plate alone, and least with strut grafting
alone.⁸⁵ Anterior plates provide
relatively similar stability, especially if augmented with a bone
graft, however, with multilevel corpectomy, anterior plate constructs
were more prone to fatigue loosening than single level corpectomies.⁷⁹
Some of the newer semiconstrained anterior plates, most of which offer
devices to lock the screws to prevent backout, allow screw rotation
which results in more load sharing with the graft.¹²⁵
By comparison, the compressive load estimated to be transmitted through
the graft increased from about 40% with a fully constrained device to
about 80% when a semiconstrained device was used.¹²⁵
Wiring or plating with lateral mass screws generally reduces
anterior-posterior motion across the fixed segment by 20% to 70%, so
none of the techniques can be considered as entirely rigid.¹¹³

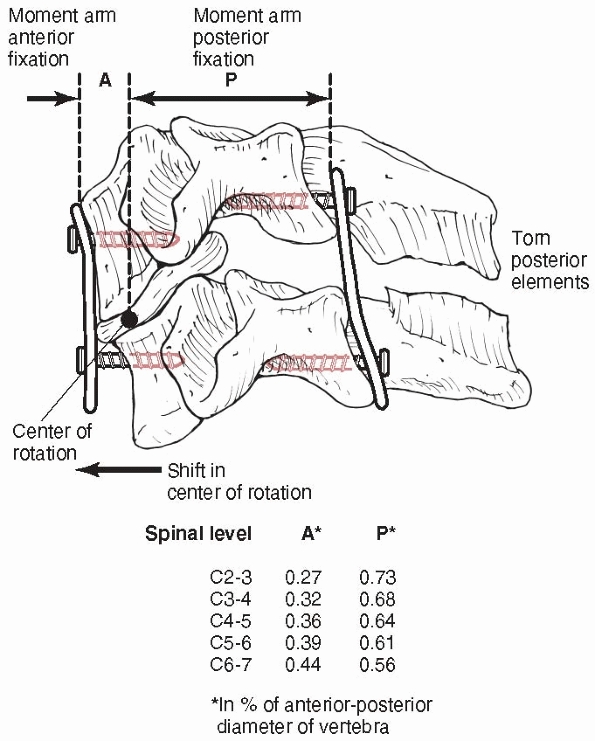FIGURE 1-55
The ratios, in terms of anterior-posterior diameter of the vertebra, of
the location of the center of rotation at each vertebral level, from
the anterior and posterior surfaces. A fixation device must resist
bending moments caused by flexion, extension, lateral bending, and
torsion. The resisting moment in the fixation is the product of the
force acting in the fixation (for example, at the screw-plate junction)
and the distance of that point on the fixation to the center of
rotation of the motion segment. The longer the moment arm for the same
bending load, the smaller the force on the fixation components.
Posterior fixation, by its location, will have lower moments in its
components.⁵

The type of attachment of the fixation system to the
vertebra is fundamental to its performance. Wires, hooks, screws, or
combinations of them all produce different types of force transfer
between the fixation and the vertebra, Figure 1-56.³⁶
A wire can resist only tension, while a screw can resist forces in all
directions (tension, compression, bending transverse to the axis of the
screw) except for rotation about its longitudinal axis. A hook only
resists forces that drive the surface of the hook against bone, and
depends also on the shape of the hook and the bone surface it rests
against. For this reason, screws are biomechanically superior to other
forms of vertebral attachments.

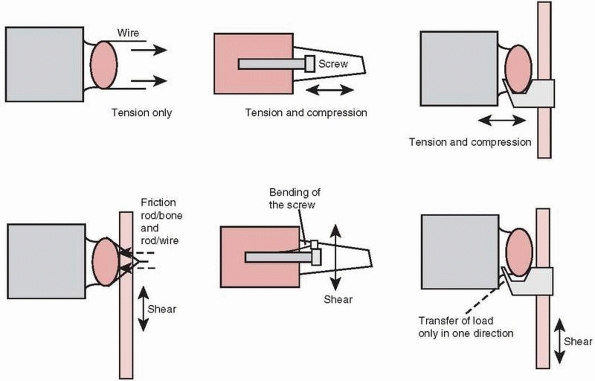FIGURE 1-56
Comparisons of the forces that can be resisted by different methods of
attachment of the fixation to the vertebra. A sublaminar wire resists
only tension, while a screw can resist forces in all directions except
for rotation about its long axis. A hook resists only forces that drive
it against the bone surfaces.

In general, pedicle screws resist pullout in the same
manner as bone screws described elsewhere, therefore pullout strength
increases with increased density of the bone it is embedded into,³³,¹⁰⁴,¹⁶¹,¹⁶⁴ a greater depth of insertion,⁹⁵ engagement of the anterior cortex,¹¹⁵
and a larger screw diameter. Single screws placed into pedicles and
loaded in a caudal-cephalad direction, which occurs during flexion and
extension of the vertebra, are vulnerable to toggling, and eventual
loosening, even under relatively small forces. As demonstrated in Figure 1-57,
the screw tends to toggle about the base of the pedicle, which is the
stiffest region, being comprised mainly of cortical bone. Toggling
tends to open the screw hole in a “windshield wiper” fashion.¹³,⁹⁵
Toggling can be reduced if the screw head is locked to the plate or
rod, and the plate or rod contacts the vertebra over a wide area.⁹⁵

Some fundamental principles should be considered when
applying lumbar spinal fixation. Longer fixation, attached to more
vertebrae, reduces forces acting on the screws because of the effect of
the greater lever arm of a longer plate or rod. A longer fusion,
although biomechanically advantageous, is not necessarily beneficial
from a clinical perspective because remaining spinal motion is
significantly reduced. Adding an anterior strut graft or a fusion cage
is important because it buttresses a posterior fixation system against
flexion moments, reducing forces in the fixation.⁸⁹
Coupler bars, which connect the fixation rods to form an H
configuration, prevent the rods from rotating medial and lateral when
torsion is applied to the motion segment, Figure 1-58. This significantly enhances the torsional and lateral bending stability of the implant.⁷²

Extensive testing has been performed on various posterior and anterior thoracolumbar fixation devices as they continue

P.35

to be developed. Testing of anterior fixation systems with and without
an augmented strut graft showed that load sharing with the graft ranged
from 63% to 89% for six systems tested, three being plates and three
based on locked rods. These tests demonstrated the significant effect
of the graft in sagittal plane stability of the fixation. The most
rigid systems, not significantly different in performance, relied on
either a thick rigid plate or large rods.²⁶
In cases of delayed or nonunion the cyclic performance of the implant
can be very important, more so than its static stiffness or maximum
load to failure. A comparison test of 12 fixation systems showed that
only three could withstand 2 million load cycles with 600N of
compressive force. The two fixations with greatest bending strength
also did not fail after cycling, however, there was no correlation
between bending strength and cyclic failure for the other 10 systems,
indicating that particular design aspects could cause fatigue failure
regardless of static strength.⁸⁸
Three devices failed in less than 10,000 cycles. Currently, most
posterior devices use essentially the same principles, including
pedicle screws with an interface clamp to the rod that allows variable
orientation of the screw, a low profile assembly, and crosslinks. They
provide similar fixation stiffness. Lumbosacral fixation using sacral
screws was most rigid and demonstrated the least screw strain when
supplemented with iliac screws, and was more effective than using
screws at S1 supplemented with screws at S2.⁹⁶

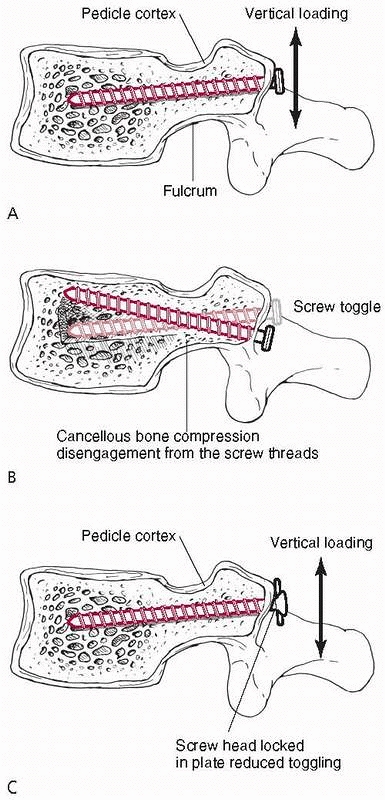FIGURE 1-57 A. The mechanism of toggling of a single pedicle screw subjected to a caudo-cephalad loading. B.
The fulcrum is at the base of the pedicle, the narrowest region with
little cancellous bone. The screw toggle compresses bone within the
vertebral body. C. Toggling is reduced if
the plate or rod to which the screw connects contacts the vertebra over
a wide surface, which prevents it from rotating, while the screw head
is locked to the plate or rod.⁹⁵

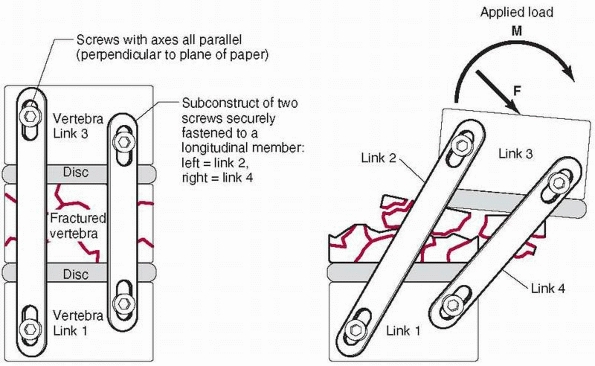FIGURE 1-58 Without a coupler bar between two longitudinal rods (left), they can rotate when a lateral moment or axial torsion is applied (right). A coupler connecting the rods to form an H configuration reduces this effect.⁷²

The biomechanical properties of fusion cages have been
investigated. A fusion cage is a hollow threaded insert that can be
applied from anterior, lateral, or posterior directions in single or
double units. Various fusion cages are available for the cervical
spine. The devices fall into one of three categories: screw designs
with a horizontal cylinder and external threads, box shapes, and
vertical cylinders. In general, all cage designs increased flexion
stiffness by 130% to 180%. Only a few box or cylinder designs increased
extension stiffness, and box designs were most effective in increasing
axial rotation and lateral bending stiffnesses, ranging from 140% to
180% of intact values.⁸² Testing of
lumbar fusion cages has shown that placement of cages in lateral,
posterolateral, or posterior orientations had little effect on
stiffness, except for torsional loading with posterior cage placement,
because posterior insertion damaged the lamina

P.36

or
facets, reducing the inherent torsional stability of the motion
segment. Fixation with cages alone did not significantly increase
lumbar motion segment stability, so augmentation with posterior
fixation in cases of motion segment instability is necessary. Because
cage fixation relies on the combination of distraction of the soft
tissues and the strength of the vertebral cancellous bone, the
properties of these tissues will have a significant effect on the
performance of cage implant constructs.¹⁵³

Fixation of the Humerus

Proximal humerus fractures fixed with locking plates
provided greater stability against torsional loading but were similar
to blade plate constructs in bending, because both fixation devices are
loaded as tension bands in bending.¹¹⁶,¹³⁷,¹³⁸
In comparing different types of blade plate constructs, the stiffest
construct employed an eight-hole, low-contact dynamic compression
plate, contoured into a blade configuration, and fixed with a diagonal
screw that triangulates with the end of the blade. This arrangement was
considerably stiffer than other blade plates or T plate and screw
constructs.¹⁰¹ One potential problem is penetration of the screws through the subchondral bone in osteoporotic patients.

SUMMARY

Effective fracture fixation requires a biomechanical
appreciation of the forces applied to a damaged bone or joint and the
basic mechanisms by which these loads are transferred through the
bridging fixation and the implant-bone interface. In particular, the
importance of the contribution of cortex-to-cortex contact across the
fracture site in resisting both compressive and bending forces must be
emphasized. This contact creates a buttress that contributes
significantly to the stability of the construct and the functional life
of the implant. Many of the observations used to formulate these basic
principles have been made using cadaveric bone in experimental
laboratory simulations, and conclusions are based on comparisons of the
most rigid mechanical construct. Other aspects such as the compromise
of blood flow or the extent of the incision during installation should
also be considered. Further, even if one construct is more rigid than
another, within a certain range of mechanical stiffness, both may
perform equally well in producing fracture healing with anatomic
alignment. It is important to correlate the biomechanical findings to
clinical observations of the performance of the implant during fracture
healing.

REFERENCES

1. Aharonoff
GB, Dennis MG, Elshinawy A, et al. Circumstances of falls causing hip
fractures in the elderly. Clin Orthop Rel Res 1998;348:10-14.

2. Allgower M. Cinderella of surgery-fractures? Surg Clin North Am 1978;58:1071-1093.

3. Alho
A, Husby T, Hoiseth A. Bone mineral content and mechanical strength. An
exvivo study on human femora at autopsy. Clin Orthop Rel Res
1988;227:292-297.

4. Ali AM, El-Shafie M, Willett KM. Failure of fixation of tibial plateau fractures. J Orthop Trauma 2002;16:323-329.

5. Amevo B, Aprill C, Bogduk N. Abnormal instantaneous axes of rotation in patients with neck pain. Spine 1992;17:748-756.

6. Aminian
A, Gao F, Fedoriw WW, et al. Vertically oriented femoral neck
fractures: mechanical analysis of four fixation techniques. J Orthop
Trauma 2007;21:544-548.

7. Antekeier
SB, Burden RL, Voor MJ, et al. Mechanical study of the safe distance
between distal femoral fracture site and distal locking screws in
antegrade intraeduallary nailing. J Orthop Trauma 2005;19:693-697.

8. Aro
HT, Wippenman BW, Hodgson SF, et al. Prediction of properties of
fracture callus by measurement of mineral density using microbone
densitometry. J Bone Jt Surg 1989;71A:1020-1030.

9. Ascenzi A, Bonucci E. The compressive properties of single osteons. Anat Rec 1968; 161:377-392.

10. Ascenzi A, Bonucci E. The shearing properties of single osteons. Anat Rec 1972;172: 499-510.

11. Ascenzi A, Bonucci E. The tensile properties of single osteons. Anat Rec 1967;158: 375-386.

12. Ascenzi A, Bonucci E, Simkin A. An approach to the mechanical properties of single osteonic lamellae. J Biomech 1973;6:227-235.

13. Ashman
RB, Galpin RD, Corin JD, et al. Biomechanical analysis of pedicle screw
instrumentation in a corpectomy model. Spine 1989;14:1398-1405.

14. Askew
MJ, Mow VC, Wirth CR, et al. Analysis of the intraosseus stress field
due to compression plating. J Biomech 1975;8:203-212.

15. Assal
M, Huber P, Rohr E, et al. Are drivers more likely to injure their
right or left foot in a frontal car crash: a car crash and
biomechanical investigation. 46th Annual Proceedings, Association for
the Advancement of Automotive Medicine 2002:273-288.

16. Augat
P, Merk J, Wolf S, et al. Mechanical stimulation by external
application of cyclic tensile strains does not effectively enhance bone
healing. J Orthop Trauma 2001;15: 54-60.

17. Ayerby
SA, Ehteshami JR, McLain RF. Offset laminar hooks decrease bending
moments of pedicle screws during in situ contouring. Spine
1997;22:376-381.

18. Bai
B, Kummer FJ, Spivak J. Augmentation of anterior vertebral body screw
fixation by an injectable biodegradable calcium phosphate bone
substitute. Spine 2001;24: 2679-2683.

19. Bartley
MH Jr., Arnold JS, Haslam RK, et al. The relationship of bone strength
and bone quantity in health, disease, and aging. J Gerontol
1996;21:517-521.

20. Behrens
F, Johnson WD. Unilateral external fixation methods to increase and
reduce frame stiffness. Clin Orthop Rel Res 1989;241:48-56.

21. Bell
GH, Dunbar O, Beck JS, et al. Variations in strength of vertebrae with
age and their relation to osteoporosis. Calcif Tissue Res 1967;1:75-86.

22. Benjamin
J, Bried J, Dohm M, et al. Biomechanical evaluation of various forms of
fixation of transverse patellar fractures. J Orthop Trauma
1987;1:219-222.

23. Black J. Orthopedic Biomaterials in Research and Practice. New York: Churchill Livingstone, 1988.

24. Beris
AE, Glisson RR, Seaber AV, et al. Load tolerance of tibial plateau
depressions reinforced with a cluster of K-wires. 34th Annual Meeting
of the Orthopedic Research Society. 1988;13:301.

25. Benirschke
SK, Swiontkowski MF. Knee. In: Hansen ST, Swiontkowski, MF, eds.
Orthopedic Trauma Protocols. New York: Raven Press, 1993.

26. Brodke
DS, Gollogly S, Bachus KN, et al. Anterior thoracolumbar
instrumentation: stiffness and load sharing characteristics of plate
and rod systems. Spine 2003: 1794-1801.

27. Brooks DB, Burstein AH, Frankel UH. The biomechanics of torsional fractures. J Bone Jt Surg 1970;52A:507-514.

28. Bucholz
RW, Ross SE, Lawrence KL. Fatigue fracture of the interlocking nail in
the treatment of fractures of the distal part of the femoral shaft. J
Bone Jt Surg 1987;69A: 1391-1399.

29. Burstein AH, Reilly DL, Martens M. Aging of bone tissue: mechanical properties. J Bone Jt Surg 1976;58A:82-86.

30. Burstein
AH, Zika IM, Heiple KG, et al. Contribution of collagen and mineral to
the elastic-plastic properties of bone. J Bone Jt Surg 1975;57A:956-961.

31. Calhoun
JH, Li F, Ledbetter BR, et al. Biomechanics of Ilizarov for fracture
fixation. 37th Annual Meeting of the Orthopedic Research Society
1991;16:439.

32. Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. J Bone Jt Surg 1977:59A:954-962.

33. Chapman
JR, Harrington RM, Lee KM, et al. Factors affecting the pullout
strength of cancellous bone screws. ASME J Biomech Eng 1996;118:391-398.

34. Clark
CR, Morgan C, Sonstegard DA, et al. The effect of biopsy-hole shape and
size on bone strength. J Bone Jt Surg 1977,59A:213-217.

35. Cody
DD, Goldstein SA, Flynn MJ, et al. Correlations between vertebral
regional bone mineral density (rBMD) and whole bone fracture load.
Spine 1991;16:146-154.

36. Coe
JD, Herzig MA, Warden KE, et al. Load to failure of spinal implants in
osteoporotic spines; a comparison of pedicle screws, laminar hooks, and
spinous process wires. 35th Annual Meeting of the Orthopedic Research
Society 1989;14:71.

37. Cordey
J, Florin P, Klaue K, et al. Compression achieved with the dynamic
compression plate: effects of the inclined sloping cylinder and
inclination of the screw. In: Uhthoff HK, ed. Current Concepts of
Internal Fixation of Fractures. Berlin: Springer-Verlag, 1980:192-200.

38. Crowninshield RD, Pope MH. The response of compact bone in tension at various strain rates. Ann Biomed Eng 1974;2:217-225.

39. Currey JD. The Mechanical Adaptation of Bones. Princeton, NJ: Princeton University Press, 1984.

40. Currey
JD. The effects of strain rate, reconstruction, and mineral content on
some mechanical properties of bovine bone. J Biomech 1975;8:81-86.

41. Currey JD. Changes in the impact energy absorption of bone with age. J Biomech 1979; 12:459-469.

42. Currey JD. The mechanical consequences of variation in the mineral content of bone. J Biomech 1969;2:1-11.

43. Currey JD, Butler G. The mechanical properties of the bone tissue in children. J Bone Jt Surg 1975;57A:810-814.

44. Dalen
N, Hellstrom LG, Jacobson B. Bone mineral content and mechanical
strength of the femoral neck. Acta Orthop Scand 1976;47:503-508.

45. DeCoster TA, Heetderks DB, Downey DJ, et al. Optimizing bone screw pullout force. J Orthop Trauma 1990;4:169-174.

46. Denny
LD, Keating EM, Engelhardt JA, et al. A comparison of fixation
techniques in tibial plateau fractures. 30th Annual Meeting of the
Orthopedic Research Society 1984; 9:314.

47. Edgarton BC, An K-A, Morrey BF. Torsional strength reduction due to cortical defects in bone. J Orthop Res 1990;8:851-855.

48. Edwards
WT, Lewallen DG, Hayes WC. The effect of pin number and fracture
pattern on immediate mechanical fixation of a subcapital hip fracture
model. 31st Annual Meeting of the Orthopedic Research Society
1985;10:219.

49. Egol
KA, Chang EY, Cvitkovic J, et al. Mismatch of current intramedullary
nails with the anterior bow of the femur. J Orthop Trauma
2004;18:410-415.

P.37

50. Egol KA, Kubiak EN, Fulkerson E, et al. Biomechanics of locked plates and screws. J Orthop Trauma 2004;18:488-493.

51. Ehmke
LW, Polzin BMI, Madey SM, et al. Femoral nailing through the
trochanter: the reamer pathway indicates a helical shaped nail. J
Orthop Trauma 2006;20:668-674.

52. Elder
S, Frankenberg E, Yetkilner DN, et al. Biomechanical evaluation of
calcium phosphate cement augmented fixation of unstable
intertrochanteric fractures. 43rd Annual Meeting of the Orthopedic
Research Society 1998;23:432.

53. Ellis
T, Bourgeault CA, Kyle RF. Screw position affects dynamic compression
plate strain in an in vitro fracture model. J Orthop Trauma
2001;15:333-337.

54. El
Maraghy AW, Elmaraghy MW, Nousiainen M, et al. Influence of the number
of cortices on the stiffness of plate fixation of diaphyseal fractures.
J Orthop Trauma 2001; 15:186-191.

55. Evans FG. Relations between the microscopic structure and tensile strength of human bone. Acta Anat 1958;35:285-301.

56. Evans
FG, Bang S. Differences and relationships between the physical
properties and the structure of human femoral, tibial, and fibular
cortical bone. Am J Anat 1967;120: 79-88.

57. Evans
FG, Vincentelli R. Relation of collagen fiber orientation to some
mechanical properties of human cortical bone. J Biomech 1969;2:63-71.

58. Finlay
JB, Jarada I, Boune RB, et al. Analysis of the pull-out strength of
screws and pegs used to secure tibial components following total knee
arthroplasty. Clin Orthop Rel Res 1989;247:220-231.

59. Frankenburg
EP, Robinson AP, Urquhart AG, et al. Supracondylar femur fractures: a
biomechanical analysis of four fixation devices. 38th Annual Meeting of
the Orthopedic Research Society 1992;17:413.

60. Frigg
R, Appenzeller A, Christensen R, et al. The development of the distal
femur Less Invasive Stabilization System (LISS). Injury
2001;32:S-C-24-31.

61. Funk JR, Tourret LJ, George SE, et al. The role of axial loading in malleolar fractures. SAE Transactions 2000-01-0155, 2000.

62. Galante J, Rostoker W, Ray RD. Physical properties of trabecular bone. Calcif Tissue Res 1970;5:236-246.

63. Geller
J, Tornetta III P, Tiburzi D, et al. Tension wire position for hybrid
external fixation of the proximal tibia. J Orthop Trauma
2000;14:502-504.

64. Georgette
FS, Sander TW, Oh I. The fatigue resistance of orthopedic wire and
cable systems. Second World Congress on Biomaterials, Washington DC,
1984:146.

65. Goldman
MW, MacLennan PA, McGwin G, et al. The association between restraint
system and upper extremity injury after motor vehicle collisions. J
Orthop Trauma 2005;19:529-534.

66. Goodman
SB, Davidson JA, Locke L, et al. A biomechanical study of two methods
of internal fixation of unstable fractures of the femoral neck. J
Orthop Trauma 1992;6: 66-72.

67. Gotfried
Y, Cohen B, Rotem A. Biomechanical evaluation of the percutaneous
compression plating system for hip fractures. J Orthop Trauma
2002;16:644-650.

68. Gotzen
L, Hutter J, Haas N. The prebending of AO plates in compression
osteosynthesis. In: Uhthoff HK, ed. Current Concepts of Internal
Fixation of Fractures. Berlin: Springer-Verlag, 1980:201-210.

69. Hansen
M, Mehler D, Hessmann MH, et al. Intramedullary stabilization of
extra-articular proximal tibial fractures: a biomechanical comparison
of intramedullary and extramedullary implants including a new proximal
tibial nail (PTN). J Orthop Trauma 2007; 21:701-709.

70. Harrell
RM, Tong J, Weinhold PS, et al. Comparison of the mechanical properties
of different tension band materials and suture techniques. J Orthop
Trauma 2003;17: 119-122.

71. Hertel
R, Jost B. Basic principles and techniques of internal fixation in
osteoporotic bone. In: Yhu An, ed. Internal Fixation in Osteoporotic
Bone. New York: Thieme, 2002:108-115.

72. Higgans
TF, Klatt J, Bachus KN. Biomechanical analysis of bicondylar tibial
plateau fixation: how does lateral locking plate fixation compare to
dual plate fixation? J Orthop Trauma 2007;21:301-306.

73. Hou
S-H, Wang J-L, Lin J. Mechanical strength, fatigue life, and failure
analysis of two prototypes and five conventional tibial locking screws.
J Orthop Res 2002;16:701-708.

74. Hufner
T, Geerling J, Oldag G, et al. Accuracy study of computer assisted
drilling: the effect of bone density, drill bit characteristics, and
use of a mechanical guide. J Orthop Trauma 2005;19:317-322.

75. Hughes
AN, Jordan BA. The mechanical properties of surgical bone screws and
some aspects of insertion practice. Injury 1972;4:25-38.

76. Hungerford DS, Barry M. Biomechanics of the patellofemoral joint. Clin Orthop Rel Res 1979;144:9-15.

77. Huiskes R, Chao EYS. Guidelines for external fixation frame rigidity and stresses. J Orthop Res 1986;4:68-75.

78. Huiskes
R, Chao EYS, Crippen TE. Parametric analyses of pin-bone stresses in
external fracture fixation. J Orthop Res 1985;3:341-349.

79. Isomi
T, Panjabi MM, Wang J-L, et al. Stabilizing potential of anterior
cervical plates in multilevel corpectomies. Spine 1999;24:2219-2223.

80. Johnson
KD, Tencer AF, Sherman MC. Biomechanical factors affecting fracture
stability and femoral bursting in closed intramedullary nailing of
femoral shaft fractures, with illustrative case presentations. J Orthop
Trauma 1987;1:1-11.

81. Kaab
MJ, Frenk A, Schmeling A, et al. Locked internal fixator, sensitivity
of screw-plate stability to the correct insertion angle of the screw. J
Orthop Trauma 2004;18: 483-487.

82. Kandziora
F, Pflugmacher R, Schafer J, et al. Biomechanical comparison of
cervical spine interbody fusion cages. Spine 2001;26:1850-1857.

83. Karnezis
IA, Miles AW, Cunningham JL, et al. Biological internal fixation of
long bone fractures: a biomechanical study of a noncontact plate
system. Injury 1998;29: 689-695.

84. Karunaker
MA, Egol KA, Peindl R, et al. Split depression tibial plateau
fractures: a biomechanical study. J Orthop Trauma 2002;16:172-177.

85. Kirkpatrick
JS, Levy JA, Carillo J, et al. Reconstruction after multilevel
corpectomy in the cervical spine. Spine 1999;24:1186-1191.

86. Klaue
K, Perren SM, Kowalski M. Internal fixation with a self-compressing
plate and screw: improvements of the plate hole and screw design. I.
Mechanical investigation. J Orthop Trauma 1991;5:280-288.

87. Korner
J, Diederichs G, Arzdorf M, et al. A biomechanical evaluation of
methods of distal humerus fracture fixation using locking compression
plates versus conventional reconstruction plates. J Orthop Trauma
2004;18:286-293.

88. Kotani
Y, Cunningham BW, Parker LM, et al. Static and fatigue biomechanical
properties of anterior thoracolumbar instrumentation systems. Spine
1999;24:1406-1413.

89. Krag MH. Biomechanics of thoracolumbar spinal fixation. A review. Spine 1991;16: S85-S98.

90. Krag
MH, Beynnan BD, Pope MH, et al. An internal fixator for posterior
application to short segments of the thoracic, lumbar, or lumbosacral
spine. Design and testing. Clin Orthop Rel Res 1986;203:75-98.

91. Krupp RJ, Malkani AL, Goodin RA, et al. Optimal entry point for retrograde femoral nailing. J Orthop Trauma 2003;17:100-105.

92. Kubiak
EN, Bong M, Park SS, et al. Intramedullary fixation of unstable
intertrochanteric hip fractures. J Orthop Trauma 2004;18:12-17.

93. Kyle
RF, Wright TM, Burstein AH. Biomechanical analysis of the sliding
characteristics of compression hip screws. J Bone Jt Surg
1980;62A:1308-1314.

94. Laurence
M, Freeman MA, Swanson SA. Engineering considerations in the internal
fixation of fractures of the tibial shaft. J Bone Jt Surg
1969;51B:754-768.

95. Law
M, Tencer AF, Anderson PA. Caudo-cephalad loading of pedicle screws:
mechanisms of loosening and methods of augmentation. Spine
1993;18:2438-2443.

96. Lebwohl
NH, Cunningham BW, Dmitriev A, et al. Biomechanical comparison of
lumbosacral fixation techniques in a calf spine model. Spine
2002;27:2312-2320.

97. Leggon
RE, Lindsey RW, Panjabi MM. Strength reduction and the effects of
treatment of long bones with diaphyseal defects involving 50% of the
cortex. J Orthop Res 1988; 6:540-546.

98. Leighton
RK, Waddell JP, Bray TJ, et al. Biomechanical testing of new and old
fixation devices for vertical shear fracture of the pelvis. J Orthop
Trauma 1991;5:313-317.

99. Liebschner
MAK, Rosenberg WS, Keaveny TM. Effects of bone cement volume and
distribution on vertebral stiffness after vertebroplasty. Spine
2001;26:1547-1554.

100. Leicher
I, Margulies JY, Weinreb A, et al. The relationship between bone
density, mineral content, and mechanical strength in the femoral neck.
Clin Orthop Rel Res 1982;163:272-281.

101. Lever
JP, Aksenov SA, Zdero R, et al. Biomechanical analysis of plate
osteosynthesis systems for proximal humerus fractures. J Orthop Trauma
2008;22:23-29.

102. Lim
TH, Breback GT, Renner SM, et al. Biomechanical evaluation of an
injectable calcium phosphate cement for vertebroplasty. Spine
2002;27:1297-1302.

103. Lotz
JC, Gerhart TN, Hayes WC. Mechanical properties of trabecular bone from
the proximal femur by single-energy quantitative computed tomography. J
Computer Assisted Tomogr 1990;14:107-114.

104. Mann
KA, Bartel DL. A structural analysis of the fixation of pedicle screws
to vertebrae. 36th Annual Meeting of the Orthopedic Research Society
1990;15:611.

105. Marti
A, Fankhauser C, Frenk A, et al. Biomechanical evaluation of the less
invasive stabilization system for the internal fixation of distal femur
fractures. J Orthop Res 2001;15:482-487.

106. McBroom,
RJ, Cheal EJ, Hayes WC. Strength reductions from metastatic cortical
defects in long bones. J Orthop Res 1988;6:369-378.

107. McKoy
BE, Conner GS, An YH. An interlocking screw for fixation in
osteoporotic bone. In: An YH, ed., Internal Fixation in Osteoporotic
Bone.New York: Thieme, 2002: 237-241.

108. McElhaney JH. Dynamic response of bone and muscle tissue. J Appl Physiol 1966;21: 1231-1236.

109. McElhaney JH, Alem NM, Roberts VL. A porous block model for cancellous bone. Am Soc Mech Eng 1970;70-WA/BHF-2:1-9.

110. McLoughlin
SW, Wheeler DL, Rider J, et al. Biomechanical evaluation of the dynamic
hip screw with two- and four-hole side plates. J Orthop Trauma
2000;14:318-323.

111. Merk BR, Stern SH, Cordes S, et al. A fatigue life analysis of small fragment screws. J Orthop Trauma 2001;15:494-499.

112. Meyer
RW, Plaxton NA, Postak PD, et al. Mechanical comparison of a distal
femoral side plate and a retrograde intramedullary nail. J Orthop
Trauma 2000;14:398-404.

113. Mihara H, Cheng BC, David SM, et al. Biomechanical comparison of posterior cervical fixation. Spine 2001;26:1662-1667.

114. Mirza SK, Moquin RR, Anderson PA, et al. Stabilizing properties of the halo apparatus. Spine 1997;22:727-733.

115. Misenhimer
GR, Peek RD, Wiltze LL, et al. Anatomic analysis of pedicle canal and
cancellous diameter related to screw size. Spine 1989;14:367-372.

116. Molloy
S, Jasper LE, Elliott DS, et al. Biomechanical evaluation of
intramedullary nail versus tension band fixation for transverse
olecranon fractures J Orthop Trauma 2004; 18:170-174.

117. Moroni
A, Aspenberg P, Toksvig-Larsen S, et al. Enhanced fixation with
hydroxapatite coated pins. Clin Orthop Rel Res 1998;346:171-177.

118. Muller ME, Allgower M, Schneider R, et al. Manual of Internal Fixation. Berlin: Springer-Verlag, 1979:85-96.

119. Nunamaker
DM, Perren SM. A radiological and histological analysis of fracture
healing using prebending of compression plates. Clin Orthop Rel Res
1979;138:167-174.

120. Ostrum
RF, Marcantonio A, Marburger R. A critical analysis of the eccentric
starting point for trochanteric intramedullary femoral nailing. J
Orthop Trauma 2005;19: 681-686.

121. Paul JP. Approaches to design, force actions transmitted by joints in the human body. Proc Roy Soc London 1976;192:163-172.

122. Perren
SM. Physical and biological aspects of fracture healing with special
reference to internal fixation. Clin Orthop Rel Res 1975;138:175-194.

123. Perren
SM, Cordey J, Baumgart F, et al. Technical and biomechanical aspects of
screws used for bone surgery. Int J Orthop Trauma 1992;2:31-48.

124. Pierce
MC, Valdevit A, Anderson L, et al. Biomechanical evaluation of dual
energy A-ray absorptiometry for predicting fracture loads of the infant
femur for injury investigation: an in vitro porcine model. J Orthop
Trauma 2000;14:571-576.

125. Rapoff AJ, Conrad BP, Johnson WM, et al. Load sharing in Premier and Zephir anterior cervical plates. Spine 2003;28:2648-2651.

126. Ratcliff
JR, Werner FW, Green JK, et al. Medial buttress versus lateral locked
plating in a cadaver medial tibial plateau fracture model. J Orthop
Trauma 2007;21:444-448.

127. Richter
M, Thermann H, Wippermann B, et al. Foot fractures in restrained front
seat car occupants: a long-term study over 23 years. J Orthop Trauma
2001;15:287-293.

128. Roberts
CS, Dodds JC, Perry K, et al. Hybrid external fixation of the proximal
tibia: strategies to improve frame stability. J Orthop Trauma
2003;17:415-420.

P.38

129. Rubin
R, Trent P, Arnold W, et al. Knowles pinning of experimental femoral
neck fractures: a biomechanical study. J Trauma 1981;21:1036-1039.

130. Russell
TA, Dingman CA, Wisnewski P. Mechanical and clinical rationale for
femoral neck fracture fixation with a cephalomedullary interlocking
nail. 37th Annual Meeting of the Orthopedic Research Society
1992;17:177.

131. Russell
TA, Taylor JC, LaVelle DG, et al. Mechanical characterization of
femoral interlocking intramedullary nailing systems. J Orthop Trauma
1991;5:332-340.

132. Sander TW, Treharne RW, Baswell I, et al. Development of a new orthopedic wire tester. J Biomed Mat Res 1983;17:587-596.

133. Sanders
R, Haidukewych GJ, Milne T, et al. Minimal versus maximal plate
fixation techniques of the ulna: the biomechanical effect of number of
screws and plate length. J Orthop Res. 2002;16:166-171.

134. Schatzker J, Sanderson R, Murnaghan JP. The holding power of orthopedic screws in vivo. Clin Orthop Rel Res 1975;108:115-126.

135. Schildhauer
TA, LeDoux WR, Chapman JR, et al. Triangular osteosynthesis and
iliosacral screw fixation for unstable sacral fractures: a cadaveric
and biomechanical evaluation under cyclic loads. J Orthop Trauma
2003;17:22-31.

136. Schawecker F. The Practise of Osteosynthesis. A Manual of Accident Surgery. Chicago: Yearbook Medical Publishers, 1974.

137. Schuster
I, Korner J, Arsdorf M, et al. Mechanical comparison in cadaver
specimens of three different 90-degree double-plate osteosyntheses for
simulated C2-type distal humerus fractures with varying bone densities.
J Orthop Trauma 2008;22:113-120.

138. Siffri
PC, Peindl RD, Coley ER, et al. Biomechanical analysis of blade plate
versus locking plate fixation for a proximal humerus fracture:
comparison using cadaveric and synthetic humeri. J Orthop Trauma
2006;20:547-554.

139. Simonian
PT, Routt ML, Harrington RM, et al. The unstable iliac fracture: a
biomechanical evaluation of internal fixation. Injury 1997;28:469-475.

140. Simonian
PT, Thomson GT, Emley W, et al. Angled screw placement in the lateral
condyle buttress plate for supracondylar femur fractures. 43th Annual
Meeting of the Orthopedic Research Society, 1998.

141. Simonian
PT, Schwappach JR, Routt Jr MLC, et al. Evaluation of new plate designs
for symphysis pubis internal fixation. J Trauma 1996;41:498-502.

142. Snow
M, Thompson G, Turner PG. A mechanical comparison of the locking
compression plate (LCP) and the low contact dynamic compression plate
(DCP) in an osteoporotic bone model. J Orthop Trauma 2008;22:121-125.

143. Spangler
L, Cummings P, Tencer AF, et al. Biomechanical factors and failure of
transcervical hip fracture repair. Injury 2001;32:223-228.

144. Spears
BR, Ostrum RF, Litsky AS. A mechanical study of gap motion in cadaver
femurs using short and long supracondylar nails. J Orthop Trauma
2004;18:354-360.

145. Stankewitz
CJ, Chapman J, Muthusamy R, et al. Relationship of mechanical factors
to the strength of proximal femur fractures fixed with cancellous
screws. J Ortho Trauma 1996;10:248-257.

146. Singh
K, Vaccaro AR, Kim J, et al. Biomechanical comparison of cervical spine
reconstructive techniques after a multilevel corpectomy of the cervical
spine. Spine 2003; 28:2352-2358.

147. Stankewich
CJ, Swiontkowski MF, Tencer AF, et al. Augmentation of femoral neck
fracture fixation with an injectable calcium-phosphate bone mineral
cement. J Orthop Res 1996;14:786-793.

148. Stone JL, Beaupre GS, Hayes WC. Multiaxial strength characteristics of trabecular bone. J Biomech 1983;16:743-752.

149. Swiontkowski
MF, Harrington RM, Keller TS, et al. Torsion and bending analysis of
internal fixation techniques for femoral neck fractures: the role of
implant design and bone density. J Orthop Res 1987;5:433-444.

150. Taitsman J, Saha S. Tensile properties of reinforced bone cement. J Bone Jt Surg 1976; 59A:419-425.

151. Tencer
AF, Asnis SE, Harrington RM, et al. Biomechanics of cannulated and
noncannulated screws. In: Asnis SE, Kyle RF, eds. Cannulated Screw
Fixation, Principles, and Operative Techniques. New York:
Springer-Verlag, 1996.

152. Tencer
AF, Claudi B, Pearce S, et al. Development of a variable stiffness
fixation system for stabilization of segmental defects of the tibia. J
Orthop Res 1984;l:395-404.

153. Tencer
AF, Hampton D, Eddy S. Biomechanical properties of threaded inserts for
lumbar interbody spinal fusion. Spine 1995;20:2408-2414.

154. Tencer
AF, Kaufman R, Ryan K, et al. Estimating the loads in femurs of
occupants in actual motor vehicle crashes using frontal crash test
data. Accident Analysis and Prevention 2002;34(1):1-11.

155. Van
Audekercke R, Martens M, Mulier JC, et al. Experimental study on
internal fixation of femoral neck fractures. Clin Orthop Rel Res
1979;141:203-212.

156. Watford
KE, Kregor PJ, Hartsock LA. LISS plate fixation of periprosthtic
supracondylar femur fractures. In: An YH, ed. Internal Fixation in
Osteoporotic Bone. New York: Thieme, 2002:271-278.

157. Weaver
JK, Chalmers J. Cancellous bone: its strength and changes with aging
and an evaluation of some methods for measuring its mineral content 1.
Age changes in cancellous bone. J Bone Jt Surg 1966:48A:289-299.

158. White
III AA, Panjabi MM, Southwick WO. Effects of compression and cyclical
loading on fracture healing—a quantitative biomechanical study. J
Biomech 1977;10:233-239.

159. White III AA, Panjabi MM, Southwick WO. The four biomechanical stages of fracture repair. J Bone Jt Surg 1977;59A:188-192.

160. Wikenheiser
MA, Lewallen DG, Markel MD. In vitro mechanical, thermal, and
microstructural performance of five external fixation pins. 38th Annual
Meeting of the Orthopedic Research Society 1992;17:409.

161. Wittenberg
RH, Shea M, Swartz DE, et al. Importance of bone mineral density in
instrumented spinal fusions. Spine 1991;16:648-652.

162. Woodard
Pl, Self J, Calhoun JH, et al. The effect of implant axial and
torsional stiffness on fracture healing. J Orthop Trauma 1987;l:33l-340.

163. Wright
TM, Hayes WC. Tensile testing of bone over a wide range of strain
rates: effects of strain rate, microstructure, and density. Med Biol
Eng 1976;14:671-680.

164. Wu
S-S, Edwards WT, Zou D, et al. Transpedicular vertebral screws in human
vertebrae: effect on screw-vertebra interface stiffness. 38th Annual
Meeting of the Orthopedic Research Society 1992;17:459.

165. Yerby
S, Scott CC, Evans NJ, et al. Effect of cutting flute design on
cortical bone screw insertion torque and pullout strength. J Orthop
Trauma 2001;15:216-221.

166. Yinger
K, Scalise J, Olson SA, et al. Biomechanical comparison of posterior
pelvic ring fixation. J Orthop Trauma 2003;17:481-487.

167. Young
JWR, Burgess AR, Brumback RJ. Lateral compression fractures of the
pelvis; the importance of plain radiographs in the diagnosis and
surgical management. Skeletal Radiol 1986:15:103-109.

168. Zand MS, Goldstein SA, Matthews LS. Fatigue failure of cortical bone screws. J Biomech 1983;16:305-311.

169. Zuber
K, Schneider E, Eulenberger J, et al. Form und Dimension der Markhohle
menschlicher Femora in Hinblick auf die Passung von
Marknagelimplantaten. Unfallchirurg 1988;91:314-319.